如何用Python蓄水池算法實現隨機抽樣

這篇文章主要介紹“如何用Python蓄水池算法實現隨機抽樣”，在日常操作中，相信很多人在如何用Python蓄水池算法實現隨機抽樣問題上存在疑惑，小編查閱了各式資料，整理出簡單好用的操作方法，希望對大家解答”如何用Python蓄水池算法實現隨機抽樣”的疑惑有所幫助！接下來，請跟著小編一起來學習吧！

現在有一組數，不知道這組數的總量有多少，請描述一種算法能夠在這組數據中隨機抽取k個數，使得每個數被取出來的概率相等。

如果這組數有n個，那么每個數字取到的概率就是k/n，但是這個問題的難點在于不知道這組數的總數，也就是不知道n，那么該怎么計算每個數取到的概率呢？

蓄水池算法

游泳池（蓄水池）大家都不陌生，有些游泳池中的水是活的，有入水管也有出水管，那么和泳池體積相當的水流過之后，是不是泳池中所有的水都會被替換呢？當然不是，有的水在泳池中可能會存留很久，有的可能剛進去就流走了。仿照這種現象，蓄水池抽樣算法誕生了，蓄水池算法的關鍵在于保證流入蓄水池的水和已經在池中的水以相同的概率留存在蓄水池中。并且蓄水池算法可以在不預先知道總量的情況下，在時間復雜度O(N)的情況下，來解決這類采樣問題。

核心原理

這一部分涉及公式，為了保證效果直接貼了圖過來。

Python實現

接下來嘗試用Python實現一下蓄水池算法，由于蓄水池算法是在事先不知道總量的情況下抽樣的，所以定義一個方法來接收單個元素，并且把這個方法放在類中，以持有采樣后的數據。

import random


class ReservoirSample(object):

    def __init__(self, size):
        self._size = size
        self._counter = 0
        self._sample = []

    def feed(self, item):
        self._counter += 1
        # 第i個元素（i <= k），直接進入池中
        if len(self._sample) <= self._size:
            self._sample.append(item)
            return self._sample
        # 第i個元素（i > k），以k / i的概率進入池中
        rand_int = random.randint(1, self._counter)
        if rand_int <= self._size:
            self._sample[rand_int - 1] = item
        return self._sample

測試代碼

接下來實現一個測試用例驗證實現的算法是否正確，既然是隨機抽樣，無法通過單詞測試來驗證是否正確，所以通過多次執行的方式來驗證，比如從1-10里隨機取樣3個數，然后執行10000次取樣，如果算法正確，最后結果中1-10被取樣的次數應該是相同的，都是3000上下。

import unittest
from collections import Counter

from reservoir_sample import ReservoirSample


class TestMain(unittest.TestCase):

    def test_reservoir_sample(self):
        samples = []
        for i in range(10000):
            sample = []
            rs = ReservoirSample(3)
            for item in range(1, 11):
                sample = rs.feed(item)
            samples.extend(sample)
        r = Counter(samples)
        print(r)

if __name__ == '__main__':
    unittest.main()

輸出的結果如下

Counter({7: 3084, 6: 3042, 10: 3033, 3: 3020, 8: 3016, 5: 2997, 4: 2986, 2: 2972, 9: 2932, 1: 2918})

上面輸出了每個數字被取樣到的次數，通過圖表可以清晰的看到分布情況

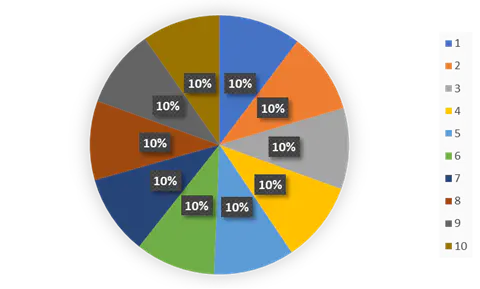
可以看出蓄水池算法對于隨機抽樣還是非常適合的，每個元素的抽樣概率都相同。

到此，關于“如何用Python蓄水池算法實現隨機抽樣”的學習就結束了，希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習，快去試試吧！若想繼續學習更多相關知識，請繼續關注億速云網站，小編會繼續努力為大家帶來更多實用的文章！