您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“Classification算法指標是什么”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
常見的分類(Classification)算法指標主要有精度(Accuracy)、準確率和召回率、ROC曲線和AUC空間這幾種。
分類是機器學習中的一類重要問題,很多重要的算法都在解決分類問題,例如決策樹,支持向量機等,其中二分類問題是分類問題中的一個重要的課題。
常見的分類模型包括:邏輯回歸、決策樹、樸素貝葉斯、SVM、神經網絡等,模型評估指標包括以下幾種:
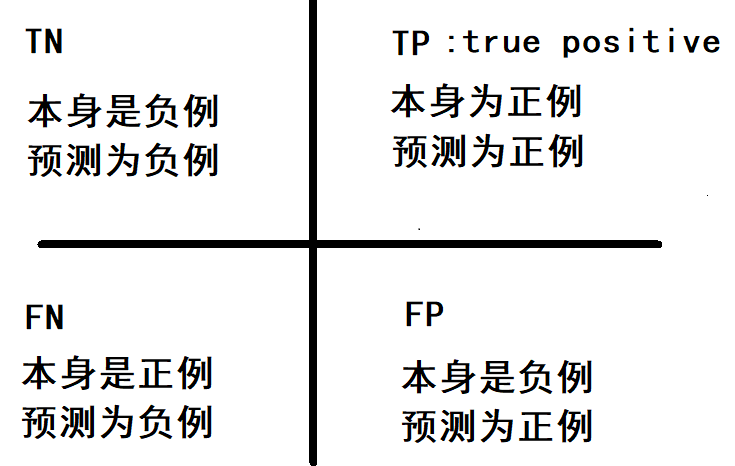
什么是混淆矩陣(Confusionmatrix)。這個名字起得是真的好,初學者很容易被這個矩陣搞得暈頭轉向。下圖a就是有名的混淆矩陣,而下圖b則是由混淆矩陣推出的一些有名的評估指標。
在二分類問題中,即將實例分成正類(positive)或負類(negative)。對一個二分問題來說,會出現四種情況。如果一個實例是正類并且也被 預測成正類,即為真正類(True positive),如果實例是負類被預測成正類,稱之為假正類(False positive)。相應地,如果實例是負類被預測成負類,稱之為真負類(True negative),正類被預測成負類則為假負類(false negative)。
True Positive (真正, TP) 被模型預測為正的正樣本;可以稱作判斷為真的正確率
True Negative (真負 , TN) 被模型預測為負的負樣本 ;可以稱作判斷為假的正確率
False Positive (假正, FP) 被模型預測為正的負樣本;可以稱作誤報率
False Negative(假負 , FN) 被模型預測為負的正樣本;可以稱作漏報率
True Positive Rate(真正率 , TPR)或靈敏度(sensitivity)
TPR = TP /(TP + FN)
正樣本預測結果數 / 正樣本實際數
True Negative Rate(真負率 , TNR)或特指度(specificity)
TNR = TN /(TN + FP)
負樣本預測結果數 / 負樣本實際數
False Positive Rate (假正率, FPR)
FPR = FP /(FP + TN)
被預測為正的負樣本結果數 /負樣本實際數
False Negative Rate(假負率 , FNR)
FNR = FN /(TP + FN)
被預測為負的正樣本結果數 / 正樣本實際數
精確度(Precision):
P = TP/(TP+FP) ; 反映了被分類器判定的正例中真正的正例樣本的比重
準確率(Accuracy)
A = (TP + TN)/(P+N) = (TP + TN)/(TP + FN + FP + TN);
反映了分類器統對整個樣本的判定能力——能將正的判定為正,負的判定為負
召回率(Recall),也稱為 True Positive Rate:
R = TP/(TP+FN) = 1 - FN/T; 反映了被正確判定的正例占總的正例的比重
from sklearn.metrics import confusion_matrix # y_pred是預測標簽 y_pred, y_true =[1,0,1,0], [0,0,1,0] confusion_matrix(y_true=y_true, y_pred=y_pred)
精確率(正確率)和召回率是廣泛用于信息檢索和統計學分類領域的兩個度量值,用來評價結果的質量。其中精度是檢索出相關文檔數與檢索出的文檔總數的比率,衡量的是檢索系統的查準率;召回率是指檢索出的相關文檔數和文檔庫中所有的相關文檔數的比率,衡量的是檢索系統的查全率。
一般來說,Precision就是檢索出來的條目(比如:文檔、網頁等)有多少是準確的,Recall就是所有準確的條目有多少被檢索出來了,兩者的定義分別如下:
Precision = 提取出的正確信息條數 / 提取出的信息條數
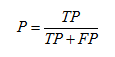
Recall = 提取出的正確信息條數 / 樣本中的信息條數
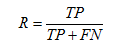
Precision和Recall指標有時候會出現的矛盾的情況,這樣就需要綜合考慮他們,最常見的方法就是在Precision和Recall的基礎上提出了F1值的概念,來對Precision和Recall進行整體評價。F1的定義如下:
F1值 = 正確率 * 召回率 * 2 / (正確率 + 召回率)
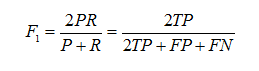
F-Measure是Precision和Recall加權調和平均:
當參數α=1時,就是最常見的F1。因此,F1綜合了P和R的結果,當F1較高時則能說明試驗方法比較有效。

準確率和召回率是互相影響的,理想情況下肯定是做到兩者都高,但是一般情況下準確率高、召回率就低,召回率低、準確率高,當然如果兩者都低,那是什么地方出問題了。當精確率和召回率都高時,F1的值也會高。在兩者都要求高的情況下,可以用F1來衡量
地震的預測
對于地震的預測,我們希望的是RECALL非常高,也就是說每次地震我們都希望預測出來。這個時候我們可以犧牲PRECISION。情愿發出1000次警報,把10次地震都預測正確了;也不要預測100次對了8次漏了兩次。
嫌疑人定罪
基于不錯怪一個好人的原則,對于嫌疑人的定罪我們希望是非常準確的。及時有時候放過了一些罪犯(recall低),但也是值得的。
不妨舉這樣一個例子:
某池塘有1400條鯉魚,300只蝦,300只鱉。現在以捕鯉魚為目的。撒一大網,逮著了700條鯉魚,200只蝦,100只鱉。那么,這些指標分別如下:
正確率 = 700 / (700 + 200 + 100) = 70%
召回率 = 700 / 1400 = 50%
F1值 = 70% * 50% * 2 / (70% + 50%) = 58.3%
不妨看看如果把池子里的所有的鯉魚、蝦和鱉都一網打盡,這些指標又有何變化:
正確率 = 1400 / (1400 + 300 + 300) = 70%
召回率 = 1400 / 1400 = 100%
F1值 = 70% * 100% * 2 / (70% + 100%) = 82.35%
由此可見,正確率是評估捕獲的成果中目標成果所占得比例;召回率,顧名思義,就是從關注領域中,召回目標類別的比例;而F值,則是綜合這二者指標的評估指標,用于綜合反映整體的指標。
當然希望檢索結果Precision越高越好,同時Recall也越高越好,但事實上這兩者在某些情況下有矛盾的。比如極端情況下,我們只搜索出了一個結果,且是準確的,那么Precision就是100%,但是Recall就很低;而如果我們把所有結果都返回,那么比如Recall是100%,但是Precision就會很低。因此在不同的場合中需要自己判斷希望Precision比較高或是Recall比較高。如果是做實驗研究,可以繪制Precision-Recall曲線來幫助分析。
代碼補充:
from sklearn.metrics import precision_score, recall_score, f1_score
# 正確率 (提取出的正確信息條數 / 提取出的信息條數)
print('Precision: %.3f' % precision_score(y_true=y_test, y_pred=y_pred))
# 召回率 (提出出的正確信息條數 / 樣本中的信息條數)
print('Recall: %.3f' % recall_score(y_true=y_test, y_pred=y_pred))
# F1-score (正確率*召回率*2 /(正確率+召回率))
print('F1: %.3f' % f1_score(y_true=y_test, y_pred=y_pred))AUC是一種模型分類指標,且僅僅是二分類模型的評價指標。AUC是Area Under Curve的簡稱,那么Curve就是ROC(Receiver Operating Characteristic),翻譯為"接受者操作特性曲線"。也就是說ROC是一條曲線,AUC是一個面積值。
ROC曲線應該盡量偏離參考線,越靠近左上越好
AUC:ROC曲線下面積,參考線面積為0.5,AUC應大于0.5,且偏離越多越好
Motivation1:在一個二分類模型中,對于所得到的連續結果,假設已確定一個閥值,比如說 0.6,大于這個值的實例劃歸為正類,小于這個值則劃到負類中。如果減小閥值,減到0.5,固然能識別出更多的正類,也就是提高了識別出的正例占所有正例 的比類,即TPR,但同時也將更多的負實例當作了正實例,即提高了FPR。為了形象化這一變化,引入ROC,ROC曲線可以用于評價一個分類器。
Motivation2:在類不平衡的情況下,如正樣本90個,負樣本10個,直接把所有樣本分類為正樣本,得到識別率為90%。但這顯然是沒有意義的。單純根據Precision和Recall來衡量算法的優劣已經不能表征這種病態問題。
繪制ROC曲線
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
# y_test:實際的標簽, dataset_pred:預測的概率值。
fpr, tpr, thresholds = roc_curve(y_test, dataset_pred)
roc_auc = auc(fpr, tpr)
#畫圖,只需要plt.plot(fpr,tpr),變量roc_auc只是記錄auc的值,通過auc()函數能計算出來
plt.plot(fpr, tpr, lw=1, label='ROC(area = %0.2f)' % (roc_auc))
plt.xlabel("FPR (False Positive Rate)")
plt.ylabel("TPR (True Positive Rate)")
plt.title("Receiver Operating Characteristic, ROC(AUC = %0.2f)"% (roc_auc))
plt.show()ROC(Receiver Operating Characteristic)翻譯為"接受者操作特性曲線"。曲線由兩個變量1-specificity 和 Sensitivity繪制. 1-specificity=FPR,即負正類率。Sensitivity即是真正類率,TPR(True positive rate),反映了正類覆蓋程度。這個組合以1-specificity對sensitivity,即是以代價(costs)對收益(benefits)。顯然收益越高,代價越低,模型的性能就越好。
此外,ROC曲線還可以用來計算“均值平均精度”(mean average precision),這是當你通過改變閾值來選擇最好的結果時所得到的平均精度(PPV)。
x 軸為假陽性率(FPR):在所有的負樣本中,分類器預測錯誤的比例

為了更好地理解ROC曲線,我們使用具體的實例來說明:
如在醫學診斷中,判斷有病的樣本。那么盡量把有病的揪出來是主要任務,也就是第一個指標TPR,要越高越好。而把沒病的樣本誤診為有病的,也就是第二個指標FPR,要越低越好。
不難發現,這兩個指標之間是相互制約的。如果某個醫生對于有病的癥狀比較敏感,稍微的小癥狀都判斷為有病,那么他的第一個指標應該會很高,但是第二個指標也就相應地變高。最極端的情況下,他把所有的樣本都看做有病,那么第一個指標達到1,第二個指標也為1。
我們以FPR為橫軸,TPR為縱軸,得到如下ROC空間。
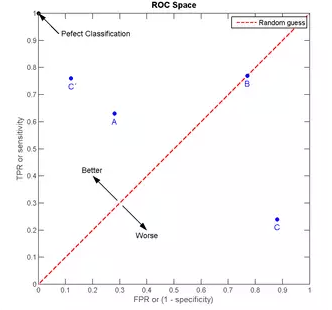
我們可以看出,左上角的點(TPR=1,FPR=0),為完美分類,也就是這個醫生醫術高明,診斷全對。點A(TPR>FPR),醫生A的判斷大體是正確的。中線上的點B(TPR=FPR),也就是醫生B全都是蒙的,蒙對一半,蒙錯一半;下半平面的點C(TPR<FPR),這個醫生說你有病,那么你很可能沒有病,醫生C的話我們要反著聽,為真庸醫。上圖中一個閾值,得到一個點。現在我們需要一個獨立于閾值的評價指標來衡量這個醫生的醫術如何,也就是遍歷所有的閾值,得到ROC曲線。
假設下圖是某醫生的診斷統計圖,為未得病人群(上圖)和得病人群(下圖)的模型輸出概率分布圖(橫坐標表示模型輸出概率,縱坐標表示概率對應的人群的數量),顯然未得病人群的概率值普遍低于得病人群的輸出概率值(即正常人診斷出疾病的概率小于得病人群診斷出疾病的概率)。
豎線代表閾值。顯然,圖中給出了某個閾值對應的混淆矩陣,通過改變不同的閾值 ,位于左下。隨著閾值的減小,紅色和綠色區域增大,紫色和藍色區域減小。閾值為 0 時,不管你什么癥狀,醫生都診斷結果都是得病(預測值都為P),此時綠色和紅色區域均占整個區域,即紫色和藍色區域的面積為 0,此時
,位于右上。
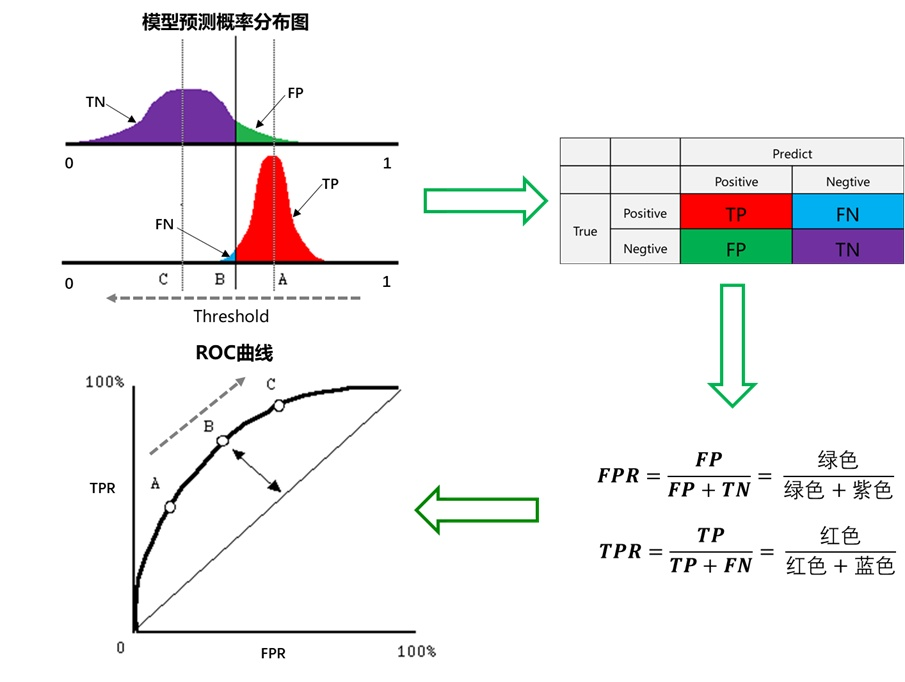
還是一開始的那幅圖,假設如下就是某個醫生的診斷統計圖,直線代表閾值。我們遍歷所有的閾值,能夠在ROC平面上得到如下的ROC曲線。
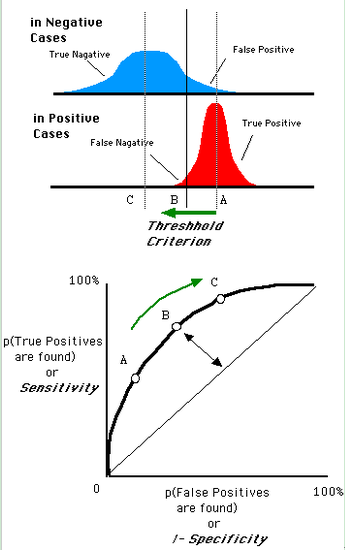
曲線距離左上角越近,證明分類器效果越好。
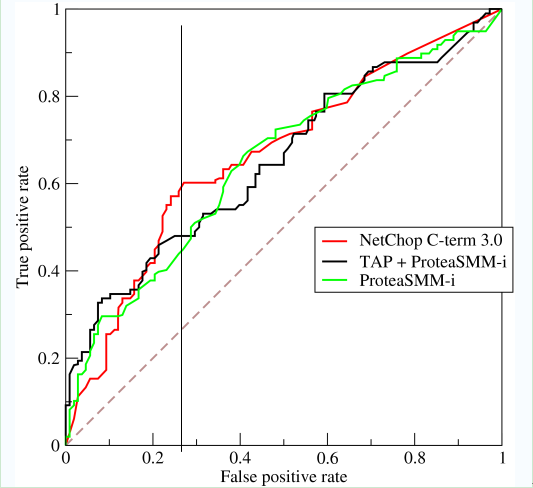
如上,是三條ROC曲線,在0.23處取一條直線。那么,在同樣的低FPR=0.23的情況下,紅色分類器得到更高的PTR。也就表明,ROC越往上,分類器效果越好。我們用一個標量值AUC來量化它。
AUC值為ROC曲線所覆蓋的區域面積,顯然,AUC越大,分類器分類效果越好。
AUC = 1,是完美分類器,采用這個預測模型時,不管設定什么閾值都能得出完美預測。絕大多數預測的場合,不存在完美分類器。
0.5 < AUC < 1,優于隨機猜測。這個分類器(模型)妥善設定閾值的話,能有預測價值。
AUC = 0.5,跟隨機猜測一樣(例:丟銅板),模型沒有預測價值。
AUC < 0.5,比隨機猜測還差;但只要總是反預測而行,就優于隨機猜測。
以下為ROC曲線和AUC值得實例:
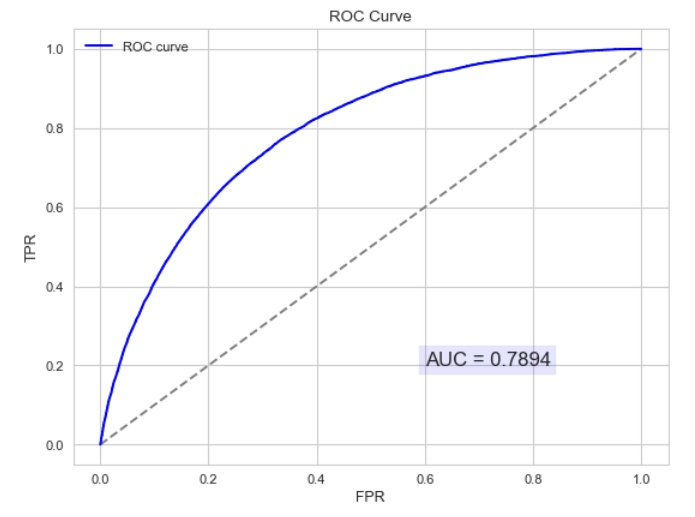
AUC的物理意義:假設分類器的輸出是樣本屬于正類的socre(置信度),則AUC的物理意義為,任取一對(正、負)樣本,正樣本的score大于負樣本的score的概率。
AUC的物理意義正樣本的預測結果大于負樣本的預測結果的概率。所以AUC反應的是分類器對樣本的排序能力。
另外值得注意的是,AUC對樣本類別是否均衡并不敏感,這也是不均衡樣本通常用AUC評價分類器性能的一個原因。
下面從一個小例子解釋AUC的含義:小明一家四口,小明5歲,姐姐10歲,爸爸35歲,媽媽33歲建立一個邏輯回歸分類器,來預測小明家人為成年人概率,假設分類器已經對小明的家人做過預測,得到每個人為成人的概率。
AUC更多的是關注對計算概率的排序,關注的是概率值的相對大小,與閾值和概率值的絕對大小沒有關系
例子中并不關注小明是不是成人,而關注的是,預測為成人的概率的排序。
第一種方法:AUC為ROC曲線下的面積,那我們直接計算面積可得。面積為一個個小的梯形面積之和。計算的精度與閾值的精度有關。
第二種方法:根據AUC的物理意義,我們計算正樣本score大于負樣本的score的概率。取N*M(N為正樣本數,M為負樣本數)個二元組,比較score,最后得到AUC。時間復雜度為O(N*M)。
第三種方法:與第二種方法相似,直接計算正樣本score大于負樣本的概率。我們首先把所有樣本按照score排序,依次用rank表示他們,如最大score的樣本,rank=n(n=N+M),其次為n-1。那么對于正樣本中rank最大的樣本,rank_max,有M-1個其他正樣本比他score小,那么就有(rank_max-1)-(M-1)個負樣本比他score小。其次為(rank_second-1)-(M-2)。最后我們得到正樣本大于負樣本的概率為

時間復雜度為O(N+M)。
from sklearn.metrics import roc_auc_score # y_test:實際的標簽, dataset_pred:預測的概率值。 roc_auc_score(y_test, dataset_pred)
“Classification算法指標是什么”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。