您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家介紹Javascript中遞歸函數的案例與代碼是怎樣的,內容非常詳細,感興趣的小伙伴們可以參考借鑒,希望對大家能有所幫助。
1、生活中的遞歸
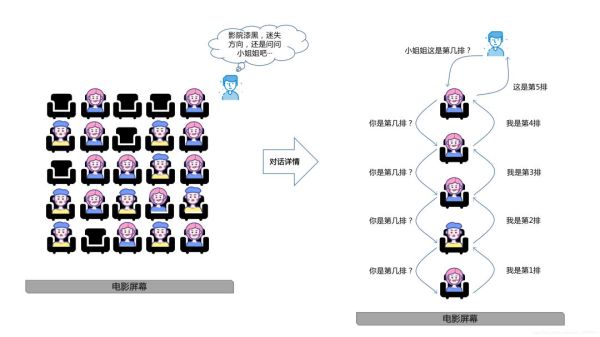
“遞歸”在生活中的一個典例就是“問路”。如圖小哥哥進入電影院后找不到自己的座位,問身邊的小姐姐“這是第幾排”,小姐姐也不清楚便依次向前詢問,問至第一排的觀眾后依次向后反饋結果,“我是第一排”,“我是第二排”,···,最終確定自己座位所在排數。
在這個過程中充分反應了“傳遞”(詢問)和“回歸”(反饋)的思想,故將這種現象稱為“遞歸”。
2、編程中的遞歸
計算機有兩個特點:“很笨”又“很快”。所以將“復雜問題”轉化為“多步驟的簡單問題”后,計算機才能高效執行。
而遞歸是編程算法的一種,通過調用自身,將一些復雜的問題簡單化,便于得出解決方案。
下面通過簡單的案例了解編程中的遞歸
案例:計算1+2+3+4+5+6的和。
function fn(n){ if(n === 1){ return 1; } return n + fn(n - 1); } fn(6);計算過程:f(6) = 6 + f(5)
f(6) = 6 + 5 + f(4)
f(6) = 6 + 5 + 4 + f(3)
f(6) = 6 + 5 + 4 + 3 + f(2)
f(6) = 6 + 5 + 4 + 3 + 2 + f(1)
f(6) = 6 + 5 + 4 + 3 + 2 + 1
由上可知遞歸函數的本質:
調用自身
遞歸函數的實現有兩個要素:
鴻蒙官方戰略合作共建——HarmonyOS技術社區
終止條件
逐步靠近終止條件
案例中的終止條件是:當 n === 1 時,fn(1) === 1。若沒有終止條件,函數會繼續計算f(0) 、f(-1) 、f(-2) ··· 從而進入死循環,無法得出結果。
通過計算過程可以看出,函數依次計算f(6)、f(5)、f(4)、f(3)、 f(2)、f(1),很好的滿足了第二個要素 逐步靠近終止條件。
通過以上講解,想必已經了解遞歸函數的原理,
那么遞歸函數是如何寫出來的呢?
如何利用遞歸函數解決實際問題呢?
實例探索遞歸函數的書寫“套路”
例題:計算n的階乘。
步驟 1:找到終止條件,寫給 if
數學知識 :n! = n * (n - 1) * (n - 2) * (n -3) * ··· * 3 * 2 * 1
顯然 終止條件 是 n === 1; 時, return 1;故可以完成函數的 前半部分:
function fn(n){ if(n === 1){ return 1; } // 未完待續 }步驟2:找到函數的等價關系式,寫給 return
數學知識 :n! = n * (n - 1)!
通過數學知識 n! = n * (n - 1)! 和遞歸函數的本質(調用自身),
可以得出函數的等價關系式為 f(n) = n * f(n - 1);
從而可以完成函數的后半部分:
function fn(n){ if(n === 1){ return 1; } return n * fn(n - 1); }至此簡單的遞歸函數便寫出來了,遞歸函數最大的特點便是代碼簡潔(簡潔到讓人心虛)。
總結,遞歸函數的書寫“套路”
1.找到終止條件,寫給 if
2.找到函數的等價關系式,寫給 return
想必你會說,上面的兩個例題用 循環 就能輕松寫出來,為何還需要使用遞歸呢?
其實能用 遞歸 解決的問題,用 循環 也能解決!而且 遞歸 比 循環 的運算速度要慢,因為 遞歸 需要逐層調用函數,占據系統內存,當 遞歸 層級較深時,對性能消耗較大,往往不推薦使用。
問:那遞歸存在的意義是什么?
遞歸 是為了將復雜問題簡單化,提供解題思路,進而得到 “循環算法”
對于簡單問題,一眼便能看出“循環算法”,但對于抽象問題,通常可以先采取 遞歸 思想,如:
例題:某人需要走上10級臺階,有兩種走法,走法A:一步1個臺階;走法B:一步2個臺階。兩種走法可以任意交替使用,問走上10級臺階共有多少種方法?

這個問題很難直接看出循環的解題思路,我們不妨從 遞歸 的角度嘗試解決:
當走上第10級臺階只差最后一步時,存在有兩種可能:
第1種:從 第8級 —> 第10級(一步2個臺階)
第2種:從 第9級 —> 第10級(一步1個臺階)
假設:從 第0級 —> 第8級,有 x 種走法;
1,1,1,1,1,1,2,2
1,1,1,1,1,2,1,2
1,2,1,1,1,2,2
1,2,1,2,2,2
·······
// 窮舉不盡,共 x 種,每種走法的最后一步都是 2(個臺階)
假設:從 第0級 —> 第9級,有 y 種走法;
1,1,1,1,1,1,1,2,1
1,1,2,1,1,2,1,1
1,2,1,2,2,1,1
1,2,2,2,2,1
·······
// 窮舉不盡,共 y 種,每種走法的最后一步都是 1(個臺階)
那么,從 第0級 —> 第10級,共有 x + y 種走法。
故,10級臺階走法 = 9級臺階走法 + 8級臺階走法,即 f(10) = f(9) + f(8);
所以我們需要的函數關系式是 f(n) = f(n - 1) + f(n - 2);
接下來找 終止條件:
1級臺階時,走法只有1種(1步1臺階),是 n === 1; 時, return 1;
2級臺階時,走法只有2種(2次1步1臺階 或 1步2臺階),是 n === 2; 時, return 2;
由此可以寫出遞歸函數
function fn(n){ if(n === 1 || n === 2){ return n; } return fun(n - 1) + fun(n - 2); }下圖展示了函數的執行過程
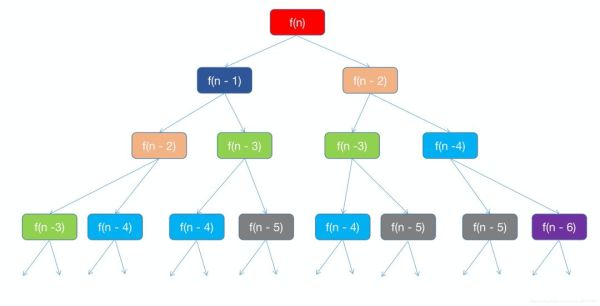
可見,在函數執行過程中重復調用了多次相同的函數(相同背景色),從而極大消耗了系統的性能。經過測試這個 遞歸函數 最多可計算至 f(45);左右的結果(測試需謹慎),這便是 遞歸函數 存在的主要問題。
那么如何優化這個問題呢?
即,將 遞歸算法改為循環算法。
通過前面的推導我們知道 f(n) = f(n - 1) + f(n - 2);
1級臺階 ==> 走法:1
2級臺階 ==> 走法:2
3級臺階 ==> 走法:1 + 2 = 3
4級臺階 ==> 走法:2 + 3 = 5
5級臺階 ==> 走法:3 + 5 = 8
6級臺階 ==> 走法:5 + 8 = 13
7級臺階 ==> 走法:8 + 13 = 21······
即,只要知道前兩項(1級臺階和2級臺階)的結果,就可以自底向上依次推算出后面所有項的結果。于是便可以寫出 循環函數
function fn(n){ if(n === 1 || n === 2){ return n; } var left = 1; // 左邊的數據 var right = 2; // 右邊的數據 var sum = 0; for(var i = 3 ; i <= n ; i++){ // 循環從第3項開始 sum = left + right; // 計算前一次左右數據的和 left = right; // 把前一次的right賦值給下一次的left right = sum; // 把前一次的和賦值給下一次的right } return sum; }以上便是通過遞歸思想將抽象問題逐步簡單化,從而得出循環算法的過程。
循環算法 解決了 遞歸 消耗系統性能的問題,可以計算任意數值。
(當數值太大超出JavaScript數值范圍時,返回 Infinity)
1、遞歸結構簡單,易理解,常用于將抽象問題簡單化。
2、遞歸要有終止條件,否則會變成死遞歸;
3、遞歸算法運行效率低、性能消耗大,遞歸深度較大時慎用(等不到結果);
4、能用遞歸解決的問題大多都能用循環解決。
關于Javascript中遞歸函數的案例與代碼是怎樣的就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。