怎么理解Java優先遍歷和廣度優先遍歷算法

這篇文章主要講解了“怎么理解Java優先遍歷和廣度優先遍歷算法”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“怎么理解Java優先遍歷和廣度優先遍歷算法”吧！

深度優先遍歷

主要思路是從圖中一個未訪問的頂點 V  開始，沿著一條路一直走到底，然后從這條路盡頭的節點回退到上一個節點，再從另一條路開始走到底...，不斷遞歸重復此過程，直到所有的頂點都遍歷完成，它的特點是不撞南墻不回頭，先走完一條路，再換一條路繼續走。

樹是圖的一種特例(連通無環的圖就是樹)，接下來我們來看看樹用深度優先遍歷該怎么遍歷。

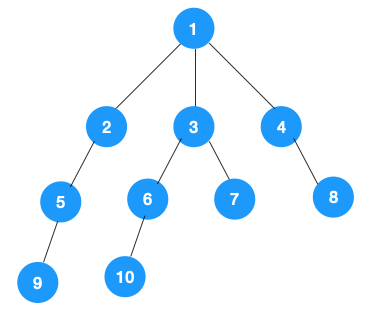
1、我們從根節點 1 開始遍歷，它相鄰的節點有 2，3，4，先遍歷節點 2，再遍歷 2 的子節點 5，然后再遍歷 5 的子節點 9。

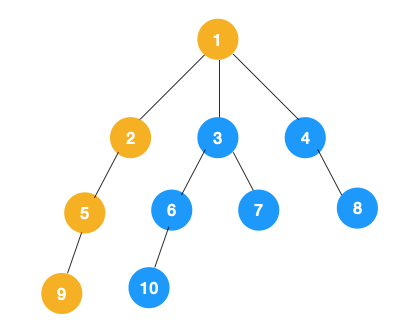
2、上圖中一條路已經走到底了(9是葉子節點，再無可遍歷的節點)，此時就從 9 回退到上一個節點 5，看下節點 5 是否還有除 9  以外的節點，沒有繼續回退到 2，2 也沒有除 5 以外的節點，回退到 1，1 有除 2 以外的節點 3，所以從節點 3 開始進行深度優先遍歷，如下：

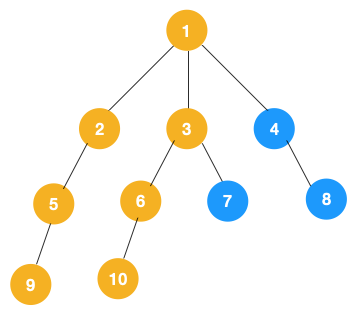
3、同理從 10 開始往上回溯到 6, 6 沒有除 10 以外的子節點，再往上回溯，發現 3 有除 6 以外的子點 7，所以此時會遍歷 7。

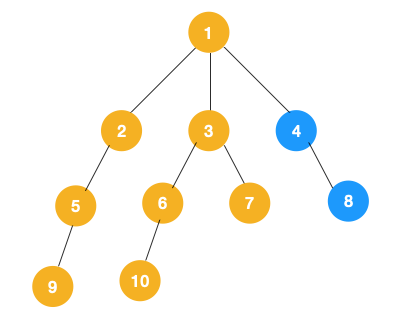
3、從 7 往上回溯到 3， 1，發現 1 還有節點 4 未遍歷，所以此時沿著 4， 8 進行遍歷,這樣就遍歷完成了。

完整的節點的遍歷順序如下(節點上的的藍色數字代表)：

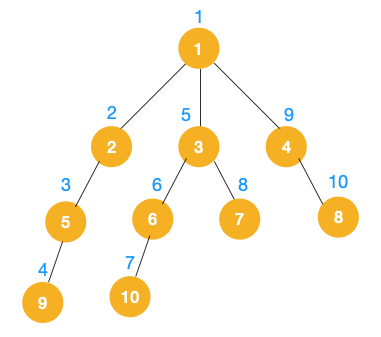
相信大家看到以上的遍歷不難發現這就是樹的前序遍歷,實際上不管是前序遍歷，還是中序遍歷，亦或是后序遍歷，都屬于深度優先遍歷。

那么深度優先遍歷該怎么實現呢，有遞歸和非遞歸兩種表現形式，接下來我們以二叉樹為例來看下如何分別用遞歸和非遞歸來實現深度優先遍歷。

1、遞歸實現

遞歸實現比較簡單，由于是前序遍歷，所以我們依次遍歷當前節點，左節點，右節點即可，對于左右節點來說，依次遍歷它們的左右節點即可，依此不斷遞歸下去，直到葉節點(遞歸終止條件)，代碼如下：

public class Solution {     private static class Node {         /**          * 節點值          */         public int value;         /**          * 左節點          */         public Node left;         /**          * 右節點          */         public Node right;          public Node(int value, Node left, Node right) {             this.value = value;             this.left = left;             this.right = right;         }     }      public static void dfs(Node treeNode) {         if (treeNode == null) {             return;         }         // 遍歷節點         process(treeNode)         // 遍歷左節點         dfs(treeNode.left);         // 遍歷右節點         dfs(treeNode.right);     } }

遞歸的表達性很好，也很容易理解，不過如果層級過深，很容易導致棧溢出。所以我們重點看下非遞歸實現。

2、非遞歸實現

仔細觀察深度優先遍歷的特點，對二叉樹來說，由于是先序遍歷(先遍歷當前節點，再遍歷左節點，再遍歷右節點)，所以我們有如下思路：

對于每個節點來說，先遍歷當前節點，然后把右節點壓棧，再壓左節點(這樣彈棧的時候會先拿到左節點遍歷，符合深度優先遍歷要求)。

彈棧，拿到棧頂的節點，如果節點不為空，重復步驟 1， 如果為空，結束遍歷。

我們以以下二叉樹為例來看下如何用棧來實現 DFS。

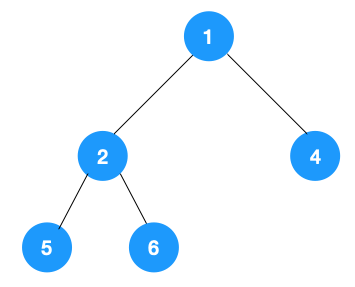
整體動圖如下：

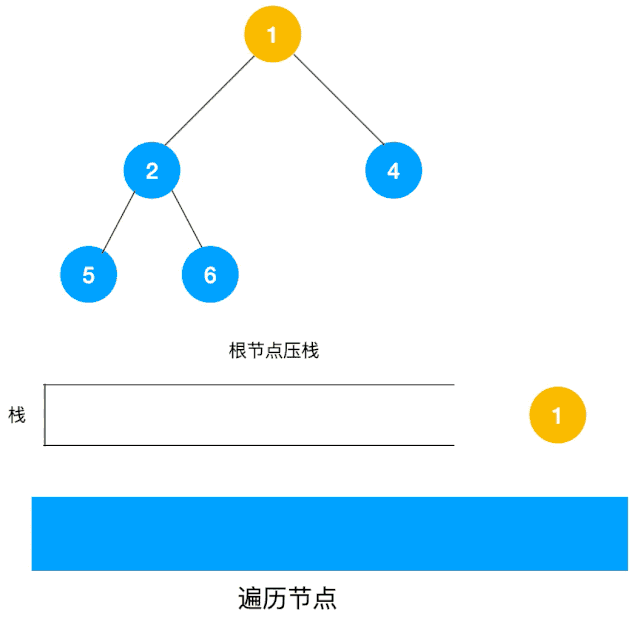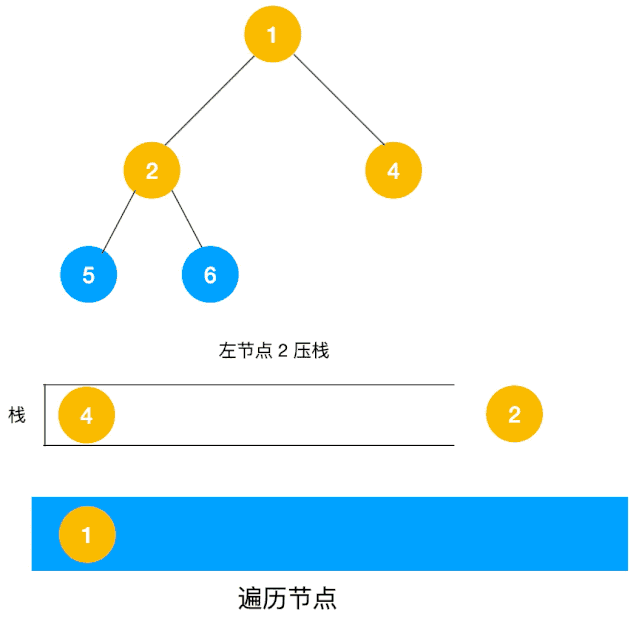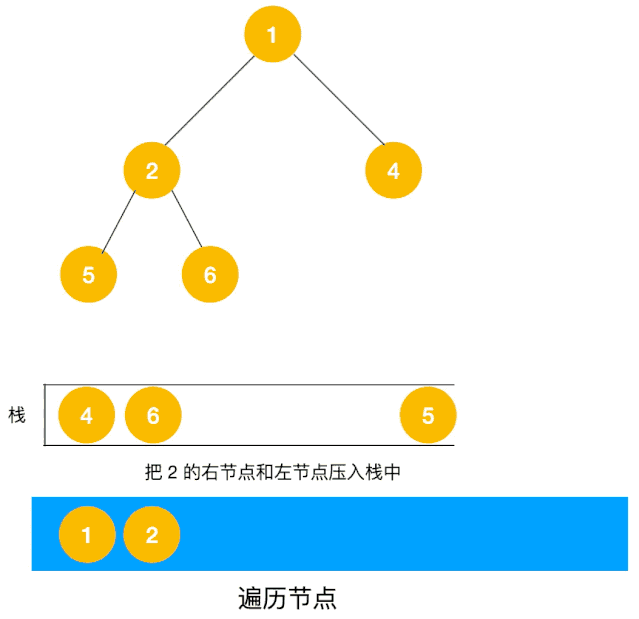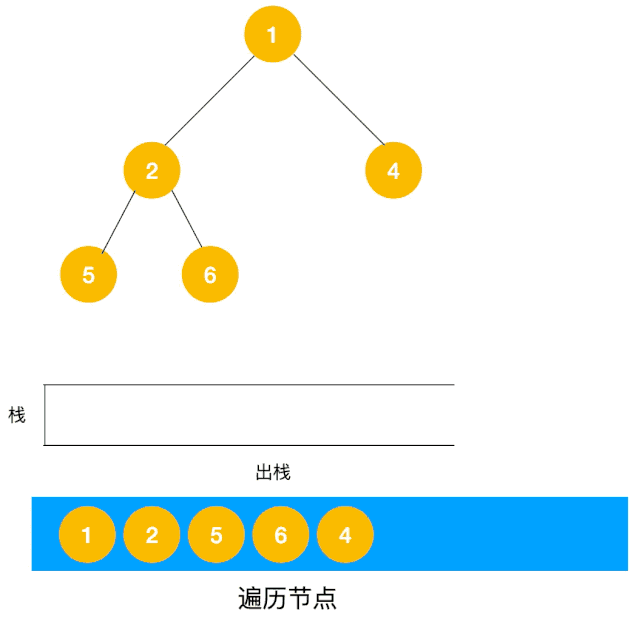
整體思路還是比較清晰的，使用棧來將要遍歷的節點壓棧，然后出棧后檢查此節點是否還有未遍歷的節點，有的話壓棧，沒有的話不斷回溯(出棧)，有了思路，不難寫出如下用棧實現的二叉樹的深度優先遍歷代碼：

/**  * 使用棧來實現 dfs  * @param root  */ public static void dfsWithStack(Node root) {     if (root == null) {         return;     }      Stack<Node> stack = new Stack<>();     // 先把根節點壓棧     stack.push(root);     while (!stack.isEmpty()) {         Node treeNode = stack.pop();         // 遍歷節點         process(treeNode)          // 先壓右節點         if (treeNode.right != null) {             stack.push(treeNode.right);         }          // 再壓左節點         if (treeNode.left != null) {             stack.push(treeNode.left);         }     } }

可以看到用棧實現深度優先遍歷其實代碼也不復雜，而且也不用擔心遞歸那樣層級過深導致的棧溢出問題。

廣度優先遍歷

廣度優先遍歷，指的是從圖的一個未遍歷的節點出發，先遍歷這個節點的相鄰節點，再依次遍歷每個相鄰節點的相鄰節點。

上文所述樹的廣度優先遍歷動圖如下，每個節點的值即為它們的遍歷順序。所以廣度優先遍歷也叫層序遍歷，先遍歷第一層(節點 1)，再遍歷第二層(節點  2，3，4)，第三層(5，6，7，8)，第四層(9，10)。

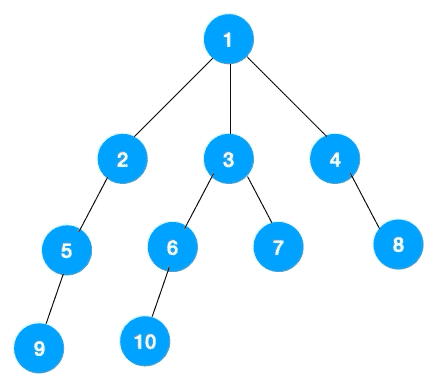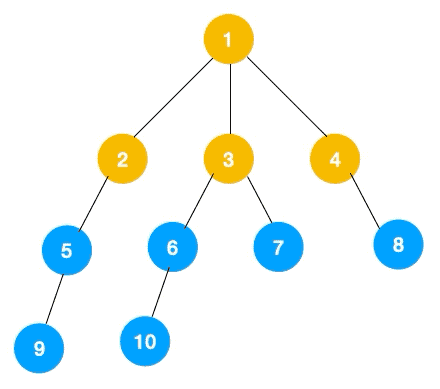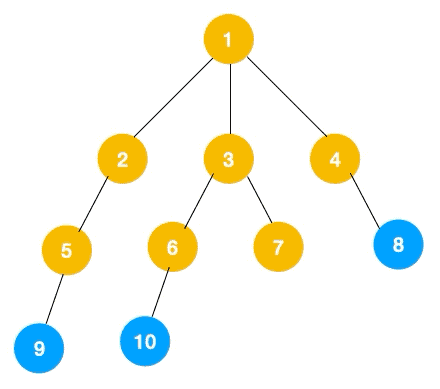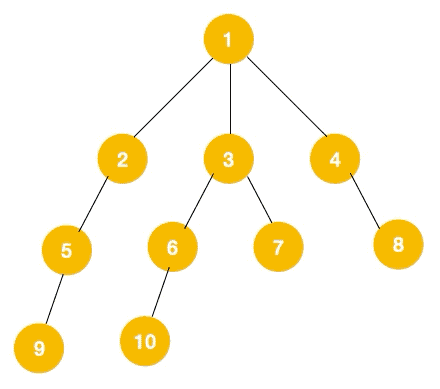
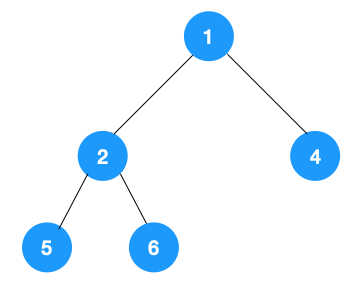
深度優先遍歷用的是棧，而廣度優先遍歷要用隊列來實現，我們以下圖二叉樹為例來看看如何用隊列來實現廣度優先遍歷。

動圖如下：

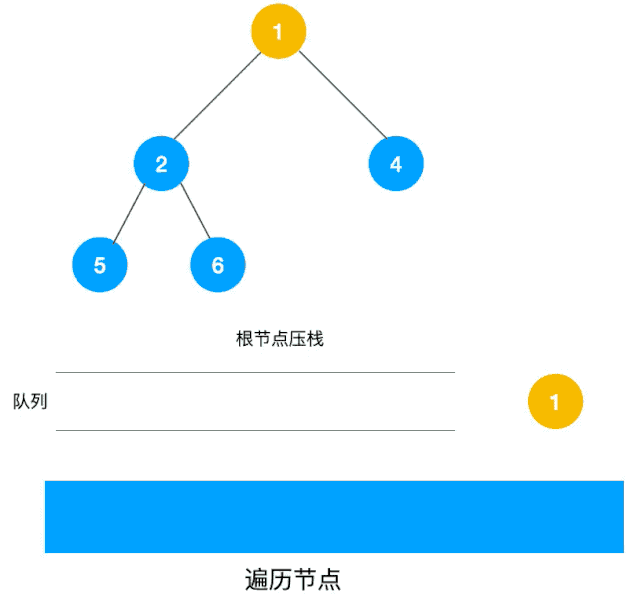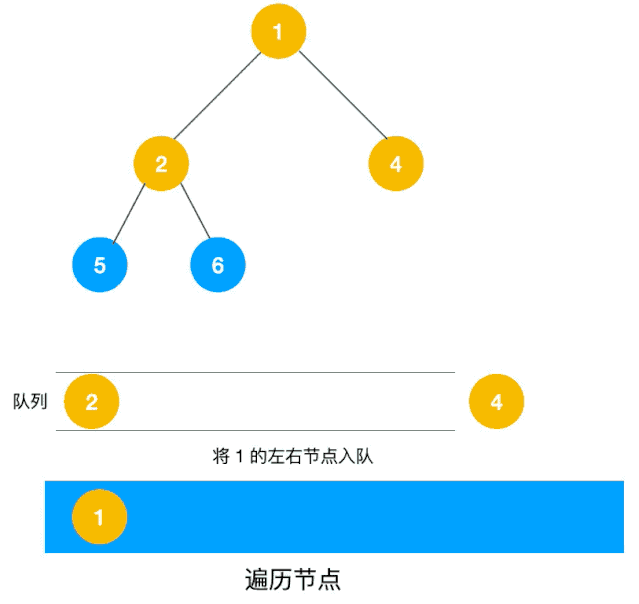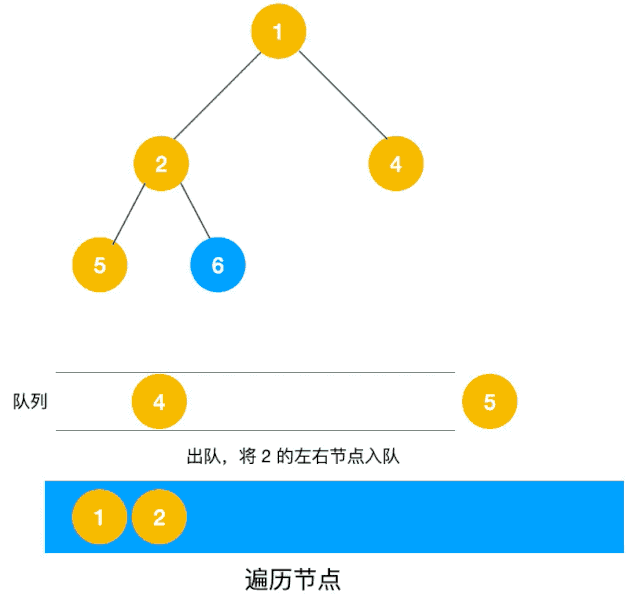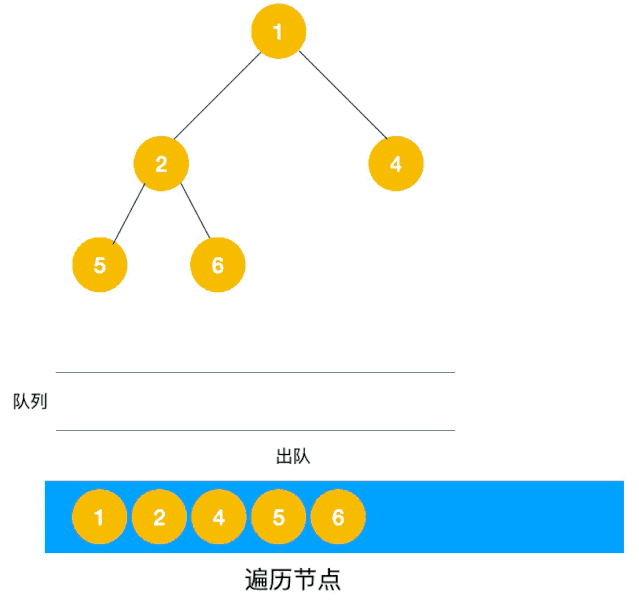
相信看了以上動圖，不難寫出如下代碼：

/**  * 使用隊列實現 bfs  * @param root  */ private static void bfs(Node root) {     if (root == null) {         return;     }     Queue<Node> stack = new LinkedList<>();     stack.add(root);      while (!stack.isEmpty()) {         Node node = stack.poll();         System.out.println("value = " + node.value);         Node left = node.left;         if (left != null) {             stack.add(left);         }         Node right = node.right;         if (right != null) {             stack.add(right);         }     } }

習題演練

接下來我們來看看在 leetcode 中出現的一些使用 DFS，BFS 來解題的題目：

leetcode 104，111: 給定一個二叉樹，找出其最大/最小深度。

例如：給定二叉樹 [3,9,20,null,null,15,7],

   3   / \  9  20    /  \   15   7

則它的最小深度 2，最大深度 3。

解題思路：這題比較簡單，只不過是深度優先遍歷的一種變形，只要遞歸求出左右子樹的最大/最小深度即可，深度怎么求，每遞歸調用一次函數，深度加一。不難寫出如下代碼：

/**  * leetcode 104: 求樹的最大深度  * @param node  * @return  */ public static int getMaxDepth(Node node) {     if (node == null) {         return 0;     }     int leftDepth = getMaxDepth(node.left) + 1;     int rightDepth = getMaxDepth(node.right) + 1;     return Math.max(leftDepth, rightDepth); }  /**  * leetcode 111: 求樹的最小深度  * @param node  * @return  */ public static int getMinDepth(Node node) {     if (node == null) {         return 0;     }     int leftDepth = getMinDepth(node.left) + 1;     int rightDepth = getMinDepth(node.right) + 1;     return Math.min(leftDepth, rightDepth); }

leetcode 102:  給你一個二叉樹，請你返回其按層序遍歷得到的節點值。(即逐層地，從左到右訪問所有節點)。示例，給定二叉樹：[3,9,20,null,null,15,7]。

   3   / \  9  20    /  \   15   7

返回其層次遍歷結果：

[   [3],   [9,20],   [15,7] ]

解題思路：顯然這道題是廣度優先遍歷的變種，只需要在廣度優先遍歷的過程中，把每一層的節點都添加到同一個數組中即可，問題的關鍵在于遍歷同一層節點前，必須事先算出同一層的節點個數有多少(即隊列已有元素個數)，因為  BFS 用的是隊列來實現的，遍歷過程中會不斷把左右子節點入隊，這一點切記!動圖如下：

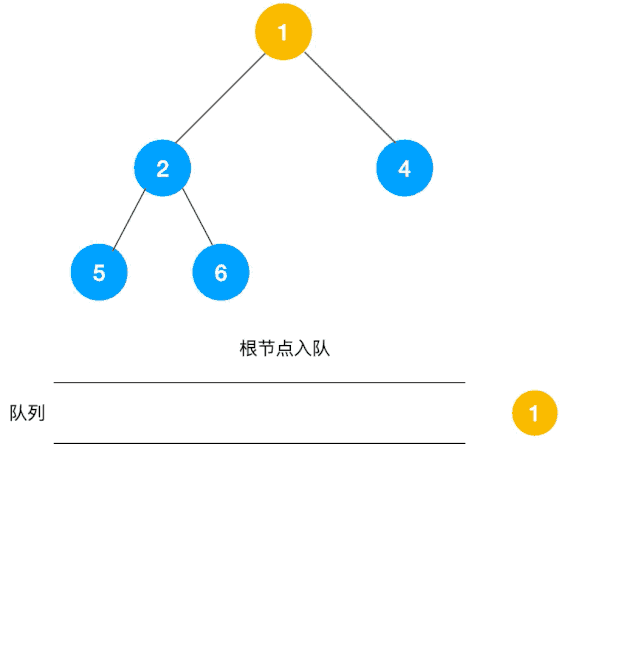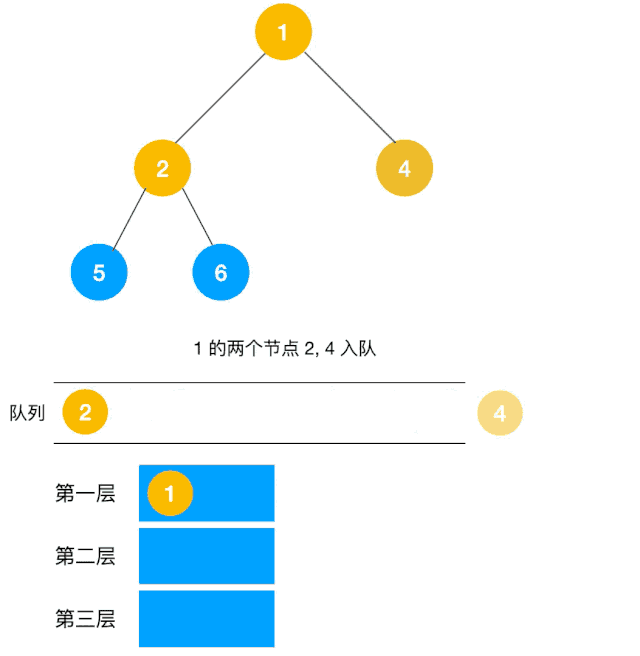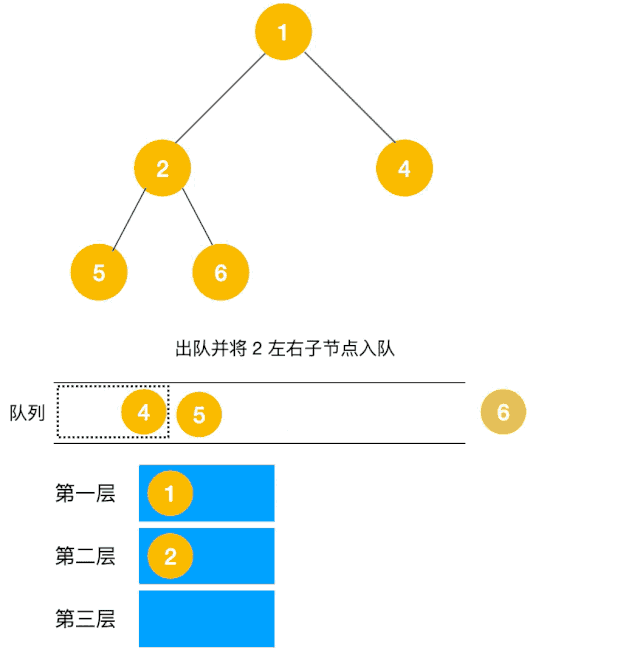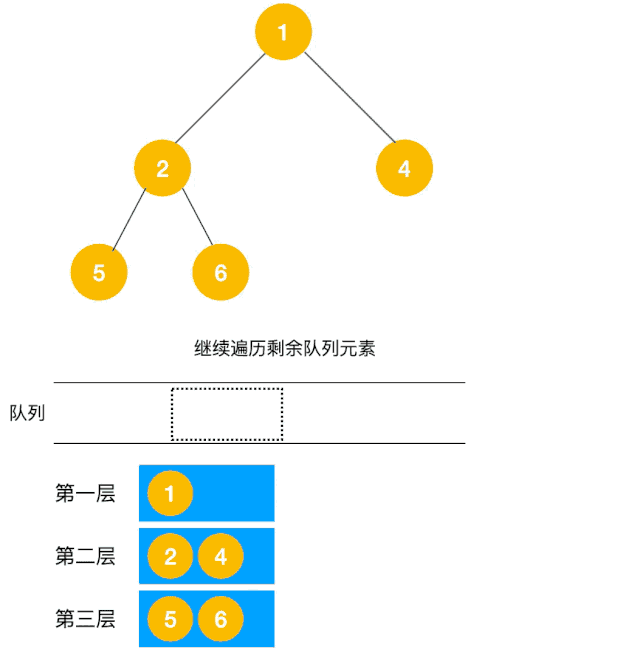
根據以上動圖思路不難得出代碼如下：

Java 代碼

/**  * leetcdoe 102: 二叉樹的層序遍歷, 使用 bfs  * @param root  */ private static List<List<Integer>> bfsWithBinaryTreeLevelOrderTraversal(Node root) {     if (root == null) {         // 根節點為空，說明二叉樹不存在，直接返回空數組         return Arrays.asList();     }      // 最終的層序遍歷結果     List<List<Integer>> result = new ArrayList<>();      Queue<Node> queue = new LinkedList<>();     queue.offer(root);      while (!queue.isEmpty()) {         // 記錄每一層         List<Integer> level = new ArrayList<>();         int levelNum = queue.size();         // 遍歷當前層的節點         for (int i = 0; i < levelNum; i++) {             Node node = queue.poll();             // 隊首節點的左右子節點入隊,由于 levelNum 是在入隊前算的，所以入隊的左右節點并不會在當前層被遍歷到             if (node.left != null) {                 queue.add(node.left);             }             if (node.right != null) {                 queue.add(node.right);             }             level.add(node.value);         }         result.add(level);     }      return result; }

Python 代碼

class Solution:     def levelOrder(self, root):         """         :type root: TreeNode         :rtype: List[List[int]]         """         res = []  #嵌套列表，保存最終結果         if root is None:             return res                  from collections import deque         que = deque([root])  #隊列，保存待處理的節點         while len(que)!=0:             lev = []  #列表，保存該層的節點的值             thislevel = len(que)  #該層節點個數             while thislevel!=0:                 head = que.popleft()  #彈出隊首節點                 #隊首節點的左右孩子入隊                 if head.left is not None:                     que.append(head.left)                 if head.right is not None:                     que.append(head.right)                 lev.append(head.val)  #隊首節點的值壓入本層                 thislevel-=1             res.append(lev)         return res

這題用 BFS 是顯而易見的，但其實也可以用 DFS， 如果在面試中能用 DFS 來處理，會是一個比較大的亮點。

用 DFS 怎么處理呢，我們知道， DFS  可以用遞歸來實現，其實只要在遞歸函數上加上一個「層」的變量即可，只要節點屬于這一層，則把這個節點放入相當層的數組里，代碼如下：

private static final List<List<Integer>> TRAVERSAL_LIST  = new ArrayList<>(); /**  * leetcdoe 102: 二叉樹的層序遍歷, 使用 dfs  * @param root  * @return  */ private static void dfs(Node root, int level) {     if (root == null) {         return;     }      if (TRAVERSAL_LIST.size() < level + 1) {         TRAVERSAL_LIST.add(new ArrayList<>());     }      List<Integer> levelList = TRAVERSAL_LIST.get(level);     levelList.add(root.value);      // 遍歷左結點     dfs(root.left, level + 1);      // 遍歷右結點     dfs(root.right, level + 1); }

DFS，BFS 在搜索引擎中的應用我們幾乎每天都在 Google, Baidu 這些搜索引擎，那大家知道這些搜索引擎是怎么工作的嗎，簡單來說有三步：

1、網頁抓取

搜索引擎通過爬蟲將網頁爬取，獲得頁面 HTML 代碼存入數據庫中

2、預處理

索引程序對抓取來的頁面數據進行文字提取，中文分詞，(倒排)索引等處理，以備排名程序使用

3、排名

用戶輸入關鍵詞后，排名程序調用索引數據庫數據，計算相關性，然后按一定格式生成搜索結果頁面。

我們重點看下第一步，網頁抓取。

這一步的大致操作如下：給爬蟲分配一組起始的網頁，我們知道網頁里其實也包含了很多超鏈接，爬蟲爬取一個網頁后，解析提取出這個網頁里的所有超鏈接，再依次爬取出這些超鏈接，再提取網頁超鏈接。。。，如此不斷重復就能不斷根據超鏈接提取網頁。如下圖示：

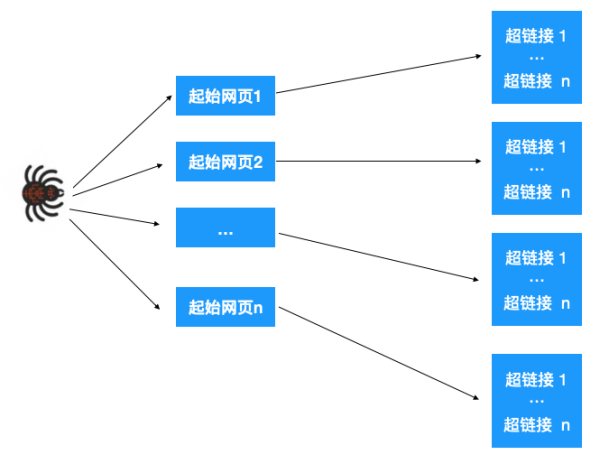
如上所示，最終構成了一張圖，于是問題就轉化為了如何遍歷這張圖，顯然可以用深度優先或廣度優先的方式來遍歷。

如果是廣度優先遍歷，先依次爬取第一層的起始網頁，再依次爬取每個網頁里的超鏈接，如果是深度優先遍歷，先爬取起始網頁  1，再爬取此網頁里的鏈接...，爬取完之后，再爬取起始網頁 2...

實際上爬蟲是深度優先與廣度優先兩種策略一起用的，比如在起始網頁里，有些網頁比較重要(權重較高)，那就先對這個網頁做深度優先遍歷，遍歷完之后再對其他(權重一樣的)起始網頁做廣度優先遍歷。

感謝各位的閱讀，以上就是“怎么理解Java優先遍歷和廣度優先遍歷算法”的內容了，經過本文的學習后，相信大家對怎么理解Java優先遍歷和廣度優先遍歷算法這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是億速云，小編將為大家推送更多相關知識點的文章，歡迎關注！