您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“關于時間復雜度的知識點有哪些”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“關于時間復雜度的知識點有哪些”吧!
究竟什么是時間復雜度
「時間復雜度是一個函數,它定性描述該算法的運行時間」。
我們在軟件開發中,時間復雜度就是用來方便開發者估算出程序運行的答題時間。
那么該如何估計程序運行時間呢,通常會估算算法的操作單元數量來代表程序消耗的時間,這里默認CPU的每個單元運行消耗的時間都是相同的。
假設算法的問題規模為n,那么操作單元數量便用函數f(n)來表示,隨著數據規模n的增大,算法執行時間的增長率和f(n)的增長率相同,這稱作為算法的漸近時間復雜度,簡稱時間復雜度,記為 O(f(n))。
什么是大O
這里的大O是指什么呢,說到時間復雜度,「大家都知道O(n),O(n^2),卻說不清什么是大O」。
算法導論給出的解釋:「大O用來表示上界的」,當用它作為算法的最壞情況運行時間的上界,就是對任意數據輸入的運行時間的上界。
同樣算法導論給出了例子:拿插入排序來說,插入排序的時間復雜度我們都說是O(n^2) 。
輸入數據的形式對程序運算時間是有很大影響的,在數據本來有序的情況下時間復雜度是O(n),但如果數據是逆序的話,插入排序的時間復雜度就是O(n^2),也就對于所有輸入情況來說,最壞是O(n^2) 的時間復雜度,所以稱插入排序的時間復雜度為O(n^2)。
同樣的同理再看一下快速排序,都知道快速排序是O(nlogn),但是當數據已經有序情況下,快速排序的時間復雜度是O(n^2) 的,「所以嚴格從大O的定義來講,快速排序的時間復雜度應該是O(n^2)」。
「但是我們依然說快速排序是O(nlogn)的時間復雜度,這個就是業內的一個默認規定,這里說的O代表的就是一般情況,而不是嚴格的上界」。如圖所示:

我們主要關心的還是一般情況下的數據形式。
「面試中說道算法的時間復雜度是多少指的都是一般情況」。但是如果面試官和我們深入探討一個算法的實現以及性能的時候,就要時刻想著數據用例的不一樣,時間復雜度也是不同的,這一點是一定要注意的。
不同數據規模的差異
如下圖中可以看出不同算法的時間復雜度在不同數據輸入規模下的差異。
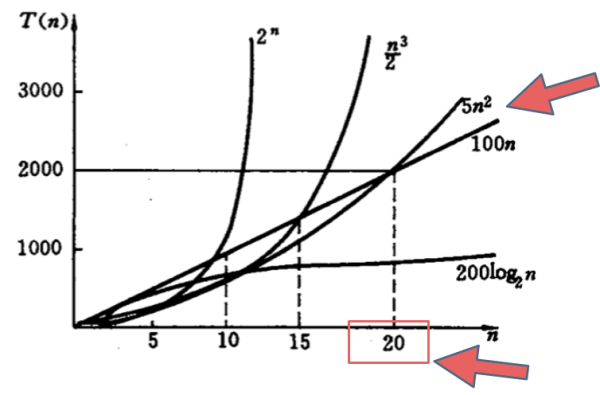
時間復雜度,不同數據規模的差異
在決定使用哪些算法的時候,不是時間復雜越低的越好(因為簡化后的時間復雜度忽略了常數項等等),要考慮數據規模,如果數據規模很小甚至可以用O(n^2)的算法比O(n)的更合適(在有常數項的時候)。
就像上圖中 O(5n^2) 和 O(100n) 在n為20之前 很明顯 O(5n^2)是更優的,所花費的時間也是最少的。
那為什么在計算時間復雜度的時候要忽略常數項系數呢,也就說O(100n) 就是O(n)的時間復雜度,O(5n^2) 就是O(n^2)的時間復雜度,而且要默認O(n) 優于O(n^2) 呢 ?
這里就又涉及到大O的定義,「因為大O就是數據量級突破一個點且數據量級非常大的情況下所表現出的時間復雜度,這個數據量也就是常數項系數已經不起決定性作用的數據量」。
例如上圖中20就是那個點,n只要大于20 常數項系數已經不起決定性作用了。
「所以我們說的時間復雜度都是省略常數項系數的,是因為一般情況下都是默認數據規模足夠的大,基于這樣的事實,給出的算法時間復雜的的一個排行如下所示」:
O(1)常數階 < O(logn)對數階 < O(n)線性階 < O(n^2)平方階 < O(n^3)(立方階) < O(2^n) (指數階)
但是也要注意大常數,如果這個常數非常大,例如10^7 ,10^9 ,那么常數就是不得不考慮的因素了。
復雜表達式的化簡
有時候我們去計算時間復雜度的時候發現不是一個簡單的O(n) 或者O(n^2), 而是一個復雜的表達式,例如:
O(2*n^2 + 10*n + 1000)
那這里如何描述這個算法的時間復雜度呢,一種方法就是簡化法。
去掉運行時間中的加法常數項 (因為常數項并不會因為n的增大而增加計算機的操作次數)。
O(2*n^2 + 10*n)
去掉常數系數(上文中已經詳細講過為什么可以去掉常數項的原因)。
O(n^2 + n)
只保留保留最高項,去掉數量級小一級的n (因為n^2 的數據規模遠大于n),最終簡化為:
O(n^2)
如果這一步理解有困難,那也可以做提取n的操作,變成O(n(n+1)) ,省略加法常數項后也就別變成了:
O(n^2)
所以最后我們說:這個算法的算法時間復雜度是O(n^2) 。
也可以用另一種簡化的思路,其實當n大于40的時候, 這個復雜度會恒小于O(3 * n^2), O(2 * n^2 + 10 * n + 1000) < O(3 * n^2),所以說最后省略掉常數項系數最終時間復雜度也是O(n^2)。
O(logn)中的log是以什么為底?
平時說這個算法的時間復雜度是logn的,那么一定是log 以2為底n的對數么?
其實不然,也可以是以10為底n的對數,也可以是以20為底n的對數,「但我們統一說 logn,也就是忽略底數的描述」。
為什么可以這么做呢?如下圖所示:

假如有兩個算法的時間復雜度,分別是log以2為底n的對數和log以10為底n的對數,那么這里如果還記得高中數學的話,應該不能理解以2為底n的對數 = 以2為底10的對數 * 以10為底n的對數。
而以2為底10的對數是一個常數,在上文已經講述了我們計算時間復雜度是忽略常數項系數的。
抽象一下就是在時間復雜度的計算過程中,log以i為底n的對數等于log 以j為底n的對數,所以忽略了i,直接說是logn。
這樣就應該不難理解為什么忽略底數了。
舉一個例子
通過這道面試題目,來分析一下時間復雜度。題目描述:找出n個字符串中相同的兩個字符串(假設這里只有兩個相同的字符串)。
如果是暴力枚舉的話,時間復雜度是多少呢,是O(n^2)么?
這里一些同學會忽略了字符串比較的時間消耗,這里并不像int 型數字做比較那么簡單,除了n^2 次的遍歷次數外,字符串比較依然要消耗m次操作(m也就是字母串的長度),所以時間復雜度是O(m * n * n)。
接下來再想一下其他解題思路。
先排對n個字符串按字典序來排序,排序后n個字符串就是有序的,意味著兩個相同的字符串就是挨在一起,然后在遍歷一遍n個字符串,這樣就找到兩個相同的字符串了。
那看看這種算法的時間復雜度,快速排序時間復雜度為O(nlogn),依然要考慮字符串的長度是m,那么快速排序每次的比較都要有m次的字符比較的操作,就是O(m * n * logn) 。
之后還要遍歷一遍這n個字符串找出兩個相同的字符串,別忘了遍歷的時候依然要比較字符串,所以總共的時間復雜度是 O(m * n * logn + n * m)。
我們對O(m * n * logn + n * m) 進行簡化操作,把m * n提取出來變成 O(m * n * (logn + 1)),再省略常數項最后的時間復雜度是 O(m * n * logn)。
最后很明顯O(m * n * logn) 要優于O(m * n * n)!
所以先把字符串集合排序再遍歷一遍找到兩個相同字符串的方法要比直接暴力枚舉的方式更快。
這就是我們通過分析兩種算法的時間復雜度得來的。
到此,相信大家對“關于時間復雜度的知識點有哪些”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。