您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“前端大數的運算及相關知識有哪些”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“前端大數的運算及相關知識有哪些”吧!
前段時間我在公司的項目中負責的是權限管理這一塊的需求。需求的大概內容就是系統的管理員可以在用戶管理界面對用戶和用戶扮演的角色進行增刪改查的操作,然后當用戶進入主應用時,前端會請求到一個表示用戶權限的數組usr_permission,前端通過usr_permission來判斷用戶是否擁有某項權限。
這個usr_permission是一個長度為16的大數字符串數組,如下所示:
const usr_permission = [ "17310727576501632001", "1081919648897631175", "4607248419625398332", "18158795172266376960", "18428747250223005711", "17294384420617192448", "216384094707056832", "13902625308286185532", "275821367043", "0", "0", "0", "0", "0", "0", "0", ]
數組中的每一個元素可以轉成64位的二進制數,二進制數中的每一位通過0和1表示一種權限,這樣每一個元素可以表示64種權限,整個usr_permission就可以表示16*64=1024種權限。后端之所以要對usr_permission進行壓縮,是因為后端采用的是微服務架構,各個模塊在通信的過程中通過在請求頭中加入usr_permission來做權限的認證。
數組usr_permission的第0個元素表示第[0, 63]號的權限,第1個元素表示第[64, 127]號的權限,以此類推。比如現在我們要查找第220號權限:
const permission = 220 // 查看銷售出庫 const usr_permission = [ "17310727576501632001", "1081919648897631175", "4607248419625398332", "18158795172266376960", "18428747250223005711", "17294384420617192448", "216384094707056832", "13902625308286185532", "275821367043", "0", "0", "0", "0", "0", "0", "0", ] // "18158795172266376960" 表示第193號~第256號權限 // 1111 1100 0000 0000 1111 1111 1111 1111 1111 0000 0000 0011 1111 1111 0000 0000 // 220 % 64 = 28 // 0000 0000 0000 0000 0000 0000 0000 1111 1100 0000 0000 1111 1111 1111 1111 1111 // 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0001 // ------------------------------------------------------------------------------- // 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0001
從usr_permission中我們得知第220號權限由第3個元素"18158795172266376960"表示。
我們將"18158795172266376960"轉成二進制得到1111 1100 0000 0000 1111 1111 1111 1111 1111 0000 0000 0011 1111 1111 0000 0000。
將220除以64得到余數28,也就是說二進制數1111 1100 0000 0000 1111 1111 1111 1111 1111 0000 0000 0011 1111 1111 0000 0000從右數的第28位表示第220號權限。
我們可以將二進制數1111 1100 0000 0000 1111 1111 1111 1111 1111 0000 0000 0011 1111 1111 0000 0000右移28位,將表示第220號權限的位數推到最低位。
然后將二進制數與1進行按位與操作,如果當前用戶擁有第220號權限,則最后得到的結果為1,反之為0。
以上就是前端查找權限的大致過程,那么這個代碼要怎么寫呢?在編寫代碼之前,我們先來復習一下JavaScript大數相關的知識,了解編寫代碼的過程中會遇到什么問題。
在計算機組成原理這門課里我們學過,在以IEEE 754為標準的浮點運算中,有兩種浮點數值表示方式,一種是單精度(32位),還有一種是雙精度(64位)。
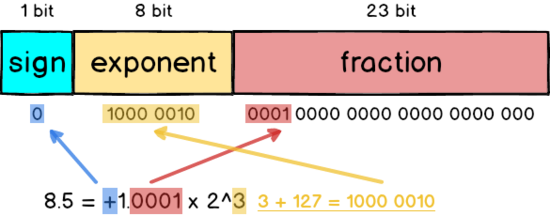
在IEEE 754標準中,一個數字被表示成 +1.0001x2^3 這種形式。比如說在單精度(32位)表示法中,有1位用來表示數字的正負(符號位),8位用來表示2的冪次方(指數偏移值E,需要減去一個固定的數字得到指數e),23位表示1后面的小數位(尾數)。
比如0 1000 0010 0001 0000 0000 0000 0000 000,第1位0表示它是正數,第[2, 9]位1000 0010轉換成十進制就是130,我們需要減去一個常數127得到3,也就是這個數字需要乘以2的三次方,第[10, 32]位則表示1.0001 0000 0000 0000 0000 000,那么這個數字表示的就是二級制中的 +1.0001*2^3 ,轉換成十進制也就是8.5。
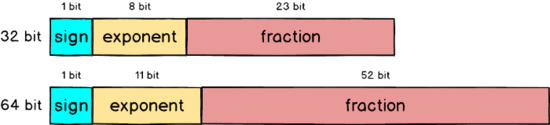
同理,雙精度(64位)也是一樣的表現形式,只是在64位中有11位用來表示2的冪次方,52位用來表示小數位。
JavaScript 就是采用IEEE754 標準定義的64 位浮點格式表示數字。在64位浮點格式中,有52位可以表示小數點后面的數字,加上小數點前面的1,就有53位可以用來表示數字,也就是說64位浮點可以表示的最大的數字是 2^53-1 ,超過 2^53-1 的數字就會發生精度丟失。因為2^53用64位浮點格式表示就變成了這樣:
符號位:0 指數:53 尾數:1.000000...000 (小數點后一共52個0)
小數點后面的第53個0已經被丟棄了,那么 2^53+1 的64位浮點格式就會變得和 2^53 一樣。一個浮點格式可以表示多個數字,說明這個數字是不安全的。所以在JavaScript中,最大的安全數是 2^53-1 ,這樣就保證了一個浮點格式對應一個數字。
有一道很常見的前端面試題,就是問你為什么JavaScript中0.1+0.2為什么不等于0.3?0.1轉換成二進制是0.0 0011 0011 0011 0011 0011 0011 ... (0011循環),0.2轉換成二進制是0.0011 0011 0011 0011 0011 0011 0011 ... (0011循環),用64位浮點格式表示如下:
// 0.1 e = -4; m = 1.1001100110011001100110011001100110011001100110011010 (52位) // 0.2 e = -3; m = 1.1001100110011001100110011001100110011001100110011010 (52位)
然后把它們相加:
e = -4; m = 1.1001100110011001100110011001100110011001100110011010 (52位) + e = -3; m = 1.1001100110011001100110011001100110011001100110011010 (52位) // 0.1和0.2指數不一致,需要進行對階操作 // 對階操作,會產生精度丟失 // 之所以選0.1進行對階操作是因為右移帶來的精度丟失遠遠小于左移帶來的溢出 e = -3; m = 0.1100110011001100110011001100110011001100110011001101 (52位) + e = -3; m = 1.1001100110011001100110011001100110011001100110011010 (52位) e = -3; m = 10.0110011001100110011001100110011001100110011001100111 (52位) // 發生精度丟失 e = -2; m = 1.00110011001100110011001100110011001100110011001100111 (53位)
我們看到已經溢出來了(超過了52位),那么這個時候我們就要做四舍五入了,那怎么舍入才能與原來的數最接近呢?比如1.101要保留2位小數,那么結果有可能是 1.10 和 1.11 ,這個時候兩個都是一樣近,我們取哪一個呢?規則是保留偶數的那一個,在這里就是保留 1.10。
回到我們之前的就是取m=1.0011001100110011001100110011001100110011001100110100 (52位)
然后我們得到最終的二進制數:
1.0011001100110011001100110011001100110011001100110100 * 2 ^ -2
=0.010011001100110011001100110011001100110011001100110100
轉換成十進制就是0.30000000000000004,所以,所以0.1 + 0.2 的最終結果是0.30000000000000004。
通過前面的講解,我們清晰地認識到在以前,JavaScript是沒有辦法對大于 2^53-1 的數字進行處理的。不過后來,JavaScript提供了內置對象BigInt來處理大數。 BigInt 可以表示任意大的整數。可以用在一個整數字面量后面加 n 的方式定義一個 BigInt ,如: 10n ,或者調用函數 BigInt() 。
const theBiggestInt = 9007199254740991n; const alsoHuge = BigInt(9007199254740991); // ? 9007199254740991n const hugeString = BigInt("9007199254740991"); // ? 9007199254740991n typeof 1n === 'bigint'; // true typeof BigInt('1') === 'bigint'; // true 0n === 0 // ? false 0n == 0 // ? true用BigInt實現的權限查找代碼如下:
hasPermission(permission: Permission) { const usr_permissions = this.userInfo.usr_permissions const arr_index = Math.floor(permission / 64) const bit_index = permission % 64 if (usr_permissions && usr_permissions.length > arr_index) { if ((BigInt(usr_permissions[arr_index]) >> BigInt(bit_index)) & 1n) { return true } } return false }但是BigInt存在兼容性問題:

根據我司用戶使用瀏覽器版本數據的分析,得到如下餅狀圖:
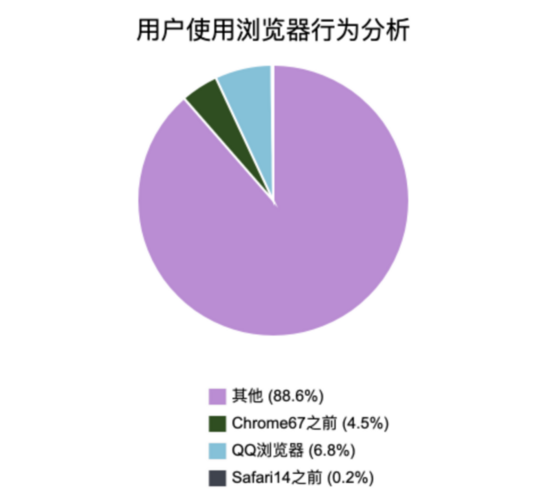
不兼容BigInt瀏覽器的比例占到12.4%
解決兼容性的問題,一種方式是如果希望在項目中繼續使用BigInt,那么需要Babel的一些插件進行轉換。這些插件需要調用一些方法去檢測運算符什么時候被用于BigInt,這將導致不可接受的性能損失,而且在很多情況下是行不通的。另外一種方法就是找一些封裝大數運算方法的第三方庫,使用它們的語法做大數運算。
很多第三方庫可以用來做大數運算,大體的思路就是定義一個數據結構來存放大數的正負及數值,分別算出每一位的結果再存儲到數據結構中。
// yarn add jsbn @types/jsbn import { BigInteger } from 'jsbn' hasPermission(permission: Permission) { const usr_permissions = this.userInfo.usr_permissions const arr_index = Math.floor(permission / 64) const bit_index = permission % 64 if (usr_permissions && usr_permissions.length > arr_index) { if ( new BigInteger(usr_permissions[arr_index]) .shiftRight(bit_index) .and(new BigInteger('1')) .toString() !== '0' ) { return true } } return false }// yarn add jsbi import JSBI from 'jsbi' hasPermission(permission: Permission) { // 開發環境不受權限限制 if (__DEVELOPMENT__) { return true } const usr_permissions = this.userInfo.usr_permissions const arr_index = Math.floor(permission / 64) const bit_index = permission % 64 if (usr_permissions && usr_permissions.length > arr_index) { const a = JSBI.BigInt(usr_permissions[arr_index]) const b = JSBI.BigInt(bit_index) const c = JSBI.signedRightShift(a, b) const d = JSBI.BigInt(1) const e = JSBI.bitwiseAnd(c, d) if (e.toString() !== '0') { return true } } return false }后來,一位同事提到了一種新的權限查找的解決方案:前端獲取到數組usr_permission以后,將usr_permission的所有元素轉成二進制,并進行字符串拼接,得到一個表示用戶所有權限的字符串permissions。當需要查找權限時,查找permissions對應的位數即可。這樣相當于在用戶進入系統時就將所有的權限都算好,而不是用一次算一次。
在中學時,我們學到的將十進制轉成二進制的方法是輾轉相除法,這里有一種新思路:
比如我們要用5個二進制位表示11這個數
我們需要先定義一個長度為5,由2的倍數組成的數組[16, 8, 4, 2, 1],然后將11與數組中的元素挨個比較
11 < 16, 所以得到[0, x, x, x, x]
11 >= 8,所以得到[0, 1, x, x, x],11 - 8 = 3
3 < 4,所以得到[0, 1, 0, x, x]
3 >= 2,所以得到[0, 1, 0, 1, x],3 - 2 = 1
1>= 1,所以得到[0, 1, 0, 1, 1],1 - 1 = 0,結束
所以用5位二進制數表示11的結果就是01011
根據上面的思路可以得到的代碼如下,這里用big.js這個包去實現:
import Big from 'big.js' import _ from 'lodash' permissions = '' // 最后生成的權限字符串 // 生成長度為64,由2的倍數組成的數組 generateBinaryArray(bits: number) { const arr: any[] = [] _.each(_.range(bits), (index) => { arr.unshift(Big(2).pow(index)) }) return arr } // 將usr_permission中單個元素轉成二進制 translatePermission(binaryArray: any[], permission: string) { let bigPermission = Big(permission) const permissionBinaryArray: number[] = [] _.each(binaryArray, (v, i) => { if (bigPermission.gte(binaryArray[i])) { bigPermission = bigPermission.minus(binaryArray[i]) permissionBinaryArray.unshift(1) } else { permissionBinaryArray.unshift(0) } }) return permissionBinaryArray.join('') } // 將usr_permission中所有元素的二進制形式進行拼接 generatePermissionString() { const usr_permissions = this.userInfo.usr_permissions let str = '' const binaryArray = this.generateBinaryArray(64) _.each(usr_permissions, (permission, index) => { str = `${str}${this.translatePermission(binaryArray, permission)}` }) this.permissions = str } // 判斷時候擁有某項權限 hasPermission(permission: Permission) { if (!this.permissions) { return false } return this.permissions[permission] === '1' }到此,相信大家對“前端大數的運算及相關知識有哪些”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。