您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
如何尋找二叉樹的下一個節點,很多新手對此不是很清楚,為了幫助大家解決這個難題,下面小編將為大家詳細講解,有這方面需求的人可以來學習下,希望你能有所收獲。
前言
已知一個包含父節點引用的二叉樹和其中的一個節點,如何找出這個節點中序遍歷序列的下一個節點?
問題分析
正如前言所述,我們的已知條件如下:
包含父節點引用的二叉樹
要查找的節點
我們要解決的問題:
找出要查找節點中序遍歷序列的下一個節點
接下來,我們通過舉例來推導下一個節點的規律,我們先來畫一顆二叉搜索樹,如下所示:
8 / \ 6 13 / \ / \ 3 7 9 15
例如,我們尋找6的下一個節點,根據中序遍歷的規則我們可知它的下一個節點是7
8的下一個節點是9
3的下一個節點是6
7的下一個節點是8
通過上述例子,我們可以分析出下述信息:
要查找的節點存在右子樹,那么它的下一個節點就是其右子樹中的最左子節點
要查找的節點不存右子樹:
當前節點屬于父節點的左子節點,那么它的下一個節點就是其父節點本身
當前節點屬于父節點的右子節點,那么就需要沿著父節點的指針一直向上遍歷,直至找到一個是它父節點的左子節點的節點
上述規律可能有點繞,大家可以將規律代入問題中多驗證幾次,就能理解了。
實現思路
二叉樹中插入節點時保存其父節點的引用
調用二叉樹的搜索節點方法,找到要查找的節點信息
判斷找到的節點是否存在右子樹
如果存在,則遍歷它的左子樹至葉節點,將其返回。
如果不存在,則遍歷它的父節點至根節點,直至找到一個節點與它父節點的左子節點相等的節點,將其返回。
實現代碼
接下來,我們將上述思路轉換為代碼,本文代碼中用到的二叉樹相關實現請移步我的另一篇文章:TypeScript實現二叉搜索樹
搜索要查找的節點
我們需要找到要查找節點在二叉樹中的節點信息,才能繼續實現后續步驟,搜索節點的代碼如下:
import { Node } from "./Node.ts"; export default class BinarySearchTree<T> { protected root: Node<T> | undefined; constructor(protected compareFn: ICompareFunction<T> = defaultCompare) { this.root = undefined; } // 搜索特定值 search(key: T): boolean | Node<T> { return this.searchNode(<Node<T>>this.root, key); } // 搜索節點 private searchNode(node: Node<T>, key: T): boolean | Node<T> { if (node == null) { return false; } if (this.compareFn(key, node.key) === Compare.LESS_THAN) { // 要查找的key在節點的左側 return this.searchNode(<Node<T>>node.left, key); } else if (this.compareFn(key, node.key) === Compare.BIGGER_THAN) { // 要查找的key在節點的右側 return this.searchNode(<Node<T>>node.right, key); } else { // 節點已找到 return node; } } }保存父節點引用
此處的二叉樹與我們實現的二叉樹稍有不同,插入節點時需要保存父節點的引用,實現代碼如下:
export default class BinarySearchTree<T> { // 插入方法 insert(key: T): void { if (this.root == null) { // 如果根節點不存在則直接新建一個節點 this.root = new Node(key); } else { // 在根節點中找合適的位置插入子節點 this.insertNode(this.root, key); } } // 節點插入 protected insertNode(node: Node<T>, key: T): void { // 新節點的鍵小于當前節點的鍵,則將新節點插入當前節點的左邊 // 新節點的鍵大于當前節點的鍵,則將新節點插入當前節點的右邊 if (this.compareFn(key, node.key) === Compare.LESS_THAN) { if (node.left == null) { // 當前節點的左子樹為null直接插入 node.left = new Node(key, node); } else { // 從當前節點(左子樹)向下遞歸,找到null位置將其插入 this.insertNode(node.left, key); } } else { if (node.right == null) { // 當前節點的右子樹為null直接插入 node.right = new Node(key, node); } else { // 從當前節點(右子樹)向下遞歸,找到null位置將其插入 this.insertNode(node.right, key); } } } } /** * 二叉樹的輔助類: 用于存儲二叉樹的每個節點 */ export class Node<K> { public left: Node<K> | undefined; public right: Node<K> | undefined; public parent: Node<K> | undefined; constructor(public key: K, parent?: Node<K>) { this.left = undefined; this.right = undefined; console.log(key, "的父節點", parent?.key); this.parent = parent; } toString(): string { return `${this.key}`; } }我們來測試下上述代碼,驗證下父節點引用是否成功:
const tree = new BinarySearchTree(); tree.insert(8); tree.insert(6); tree.insert(3); tree.insert(7); tree.insert(13); tree.insert(9); tree.insert(15);
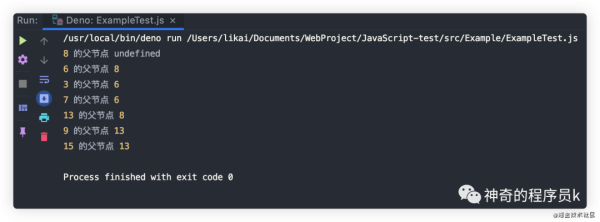
在保存父節點引用時折騰了好久也沒實現,最后求助了我的朋友_Dreams?。
尋找下一個節點
接下來,我們就可以根據節點的規律來實現這個算法了,實現代碼如下:
export class TreeOperate<T> { /** * 尋找二叉樹的下一個節點 * 規則: * 1. 輸入一個包含父節點引用的二叉樹和其中的一個節點 * 2. 找出這個節點中序遍歷序列的下一個節點 * * 例如: * 8 * / \ * 6 13 * / \ / \ * 3 7 9 15 * * 6的下一個節點是7,8的下一個節點是9 * * 通過分析,我們可以得到下述信息: * 1. 如果一個節點有右子樹,那么它的下一個節點就是其右子樹中的最左子節點 * 2. 如果一個節點沒有右子樹: * (1). 當前節點屬于父節點的左子節點,那么它的下一個節點就是其父節點本身 * (2). 當前節點屬于父節點的右子節點,沿著父節點的指針一直向上遍歷,直至找到一個是它父節點的左子節點的節點 * */ findBinaryTreeNextNode(tree: BinarySearchTree<number>, node: number): null | Node<number> { // 搜索節點 const result: Node<number> | boolean = tree.search(node); if (result == null) throw "節點不存在"; let currentNode = result as Node<number>; // 右子樹存在 if (currentNode.right) { currentNode = currentNode.right; // 取右子樹的最左子節點 while (currentNode.left) { currentNode = currentNode.left; } return currentNode; } // 右子樹不存在 while (currentNode.parent) { // 當前節點等于它父節點的左子節點則條件成立 if (currentNode === currentNode.parent.left) { return currentNode.parent; } // 條件不成立,繼續獲取它的父節點 currentNode = currentNode.parent; } return null; } }我們通過一個例子來測試下上述代碼:
// 構建二叉搜索樹 const tree = new BinarySearchTree(); tree.insert(8); tree.insert(6); tree.insert(3); tree.insert(7); tree.insert(13); tree.insert(9); tree.insert(15); // 尋找下一個節點 const nextNode = treeOperate.findBinaryTreeNextNode(tree, 7); console.log("7的下一個節點", nextNode.toString());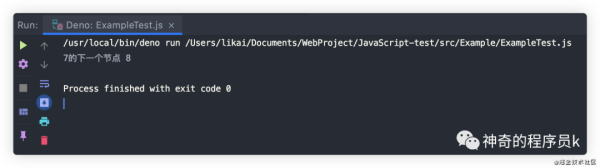
代碼地址
文中完整代碼如下:
TreeOperate.ts
BinarySearchTree.ts
看完上述內容是否對您有幫助呢?如果還想對相關知識有進一步的了解或閱讀更多相關文章,請關注億速云行業資訊頻道,感謝您對億速云的支持。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。