您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“什么是赫夫曼編碼”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
赫夫曼編碼也翻譯為(哈夫曼編碼)Huffman Coding,又稱為霍夫曼編碼,是一種編碼方式,屬于一種程序算法。
赫夫曼編碼是赫夫曼樹在電訊通訊中的經典的應用場景之一。
赫夫曼編碼廣泛的用于數據文件壓縮。其壓縮率通常在20%~90%之間。
赫夫曼碼是可變字長編碼(VLC)的一種.Hufuuman于1952年提出一種編碼方法,稱之為最佳編碼。
如: i like like like java do you like a java 共40個字符,包括空格,其對應的ASCII碼,與二進制編碼如下圖

按照二進制來傳遞信息,總的長度是359(包含空格)
i like like like java do you like a java 共40個字符,包括空格。變長編碼處理如下圖

字符的編碼都不能是其他字符編碼的前綴,符合此要求的編碼叫做前綴編碼,即不能匹配到重復的編碼。
i like like like java do you like a java 共40個字符,包括空格。變長編碼處理如下圖

按照上面字符出現的次數構建一顆赫夫曼樹,次數作為權值。
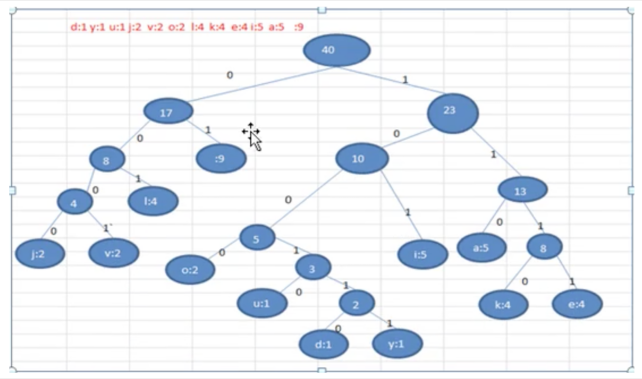
根據赫夫曼樹,給各個字符,規定編碼(前綴編碼),向左的路徑為0 向右的路徑為1:編碼如下:
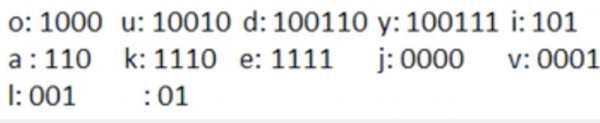
按照上面的赫夫曼編碼,我們的"i like like like java do you like a java" 字符串對應的編碼(注意這里我們使用的無損壓縮)如下圖。

原來的長度是359,壓縮了(359-133)/359=62.9%
此編碼滿足前綴編碼,即字符的編碼都不能是其他字符編碼的前綴。不會造成匹配的多義性。
赫夫曼編碼是無損壓縮!!
這個赫夫曼樹根據排序方法不同,也可能不一樣,這樣對應的赫夫曼編碼也不完全一樣,但是wpl是一樣的,都是最小的,比如我們讓每次生成的新的二叉樹總是排在權值相同的二叉樹的最后一個,則生成的二叉樹為:
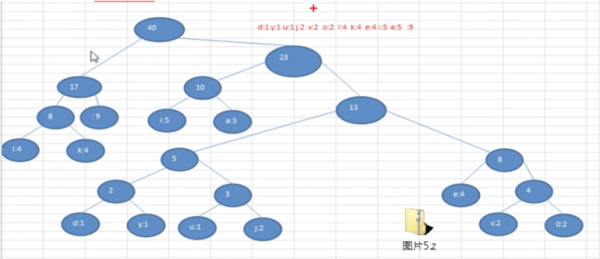
根據赫夫曼編碼壓縮數據的原理,需要創建"i like like like java do you like a java" 對應的赫夫曼樹
先創建Node節點,Node {data{存放數據},weight(權值),left,right};
得到"i like like like java do you like a java" 對應的byte[] 數組;
編寫一個方法,將準備構建赫夫曼樹的node節點放到List
可以通過集合List
將一串字符串進行壓縮與解壓縮
package com.xie.huffmancode; import java.util.*; public class HuffmanCode { public static void main(String[] args) { String str = "i like like like java do you like a java"; byte[] contentBytes = str.getBytes(); System.out.println("contentBytes=" + Arrays.toString(contentBytes)); List<Node> nodes = getNodes(contentBytes); //生成赫夫曼樹 Node hufffmanTreeRoot = createHufffmanTree(nodes); //生成的赫夫曼編碼表 getCodes(hufffmanTreeRoot, "", stringBuilder); byte[] huffmanCodeBytes = zip(contentBytes, huffmanCodes); System.out.println("huffmanCodeBytes = " + Arrays.toString(huffmanCodeBytes)); byte[] decode = decode(huffmanCodes, huffmanCodeBytes); System.out.println("赫夫曼解碼后對應的數組" + new String(decode)); /** * contentBytes=[105, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 108, 105, 107, 101, 32, 106, 97, 118, 97, 32, 100, 111, 32, 121, 111, 117, 32, 108, 105, 107, 101, 32, 97, 32, 106, 97, 118, 97] * huffmanCodeBytes = [-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28] * 赫夫曼解碼后對應的數組i like like like java do you like a java */ } //完成數據的解壓思路 //1.將huffmanCodeBytes[-88, -65, -56, -65, -56, -65, -55, 77, -57, 6, -24, -14, -117, -4, -60, -90, 28] // 重新轉成 赫夫曼編碼對應的二進制字符串"101010001011111111001000101111...." //2.赫夫曼編碼對應的二進制字符串"101010001011111111001000101111...." => 對照赫夫曼編碼表 => "i like like like java do you like a java" /** * 完成對壓縮數據的解碼 * * @param huffmanCodes 赫夫曼編碼表 * @param huffmanBytes 赫夫曼編碼得到的字節數組 * @return 原來的字符串對應的數組 */ public static byte[] decode(Map<Byte, String> huffmanCodes, byte[] huffmanBytes) { StringBuilder stringBuilder = new StringBuilder(); for (int i = 0; i < huffmanBytes.length; i++) { //判斷是不是最后一個字節 boolean flag = (i == huffmanBytes.length - 1); stringBuilder.append(byteToBitString(!flag, huffmanBytes[i])); } Map<String, Byte> map = new HashMap<>(); for (Map.Entry<Byte, String> entry : huffmanCodes.entrySet()) { Byte k = entry.getKey(); String v = entry.getValue(); map.put(v, k); } List<Byte> list = new ArrayList<>(); for (int i = 0; i < stringBuilder.length();) { int count = 1; boolean flag = true; Byte b = null; while (flag) { String key = stringBuilder.substring(i, i + count);//i 不動,count移動,直到匹配一個字符 b = map.get(key); if (b == null) { count++; } else { flag = false; } } list.add(b); i += count; } byte[] bytes = new byte[list.size()]; for (int i = 0; i < list.size(); i++) { bytes[i] = list.get(i); } return bytes; } /** * 將一個byte 轉成一個二進制的字符串 * * @param flag 標識是否需要補高位,true標識需要補高位,如果是false表示不補,如果是最后一個字節,無需補高位 * @param b 傳入的byte * @return 該byte對應的二進制字符串,(注意是按補碼返回) */ public static String byteToBitString(boolean flag, byte b) { //將b 轉成 int int temp = b; //如果temp是正數還需要補高位 if (flag) { // 按位或 如 256|1=> 1 0000 0000|0000 0001 => 1 0000 0001 temp |= 256; } //返回的是temp二進制的補碼 String bitStr = Integer.toBinaryString(temp); if (flag) { //取后8位 return bitStr.substring(bitStr.length() - 8); } else { return bitStr; } } /** * 封裝原始字節數組轉赫夫曼字節數組 * * @param bytes * @return */ public static byte[] huffmanZip(byte[] bytes) { List<Node> nodes = getNodes(bytes); //創建赫夫曼樹 Node hufffmanTreeRoot = createHufffmanTree(nodes); //生成赫夫曼編碼 getCodes(hufffmanTreeRoot, "", stringBuilder); //返回壓縮后的赫夫曼編碼字節數組 return zip(bytes, huffmanCodes); } /** * 將字符串對應的byte[] 數組,通過赫夫曼編碼表,返回一個赫夫曼編碼壓縮后的byte[] * * @param bytes 原始字符串對應的byte[] * @param huffmanCodes 生成的赫夫曼編碼 * @return 返回赫夫曼編碼處理后的byte[] */ public static byte[] zip(byte[] bytes, Map<Byte, String> huffmanCodes) { //利用huffmanCodes 將 bytes 轉成赫夫曼編碼對應的字符串 StringBuilder stringBuilder = new StringBuilder(); for (byte b : bytes) { stringBuilder.append(huffmanCodes.get(b)); } // 將"101010001011111111001000101111...." 轉成byte[] // 統計返回byte[] huffmanCodeBytes 長度 int len; if (stringBuilder.length() % 8 == 0) { len = stringBuilder.length() / 8; } else { len = stringBuilder.length() / 8 + 1; } //創建 存儲壓縮后的byte[]數組 byte[] huffmanCodeBytes = new byte[len]; int index = 0; for (int i = 0; i < stringBuilder.length(); i += 8) { String strByte; if (i + 8 > stringBuilder.length()) { strByte = stringBuilder.substring(i); } else { strByte = stringBuilder.substring(i, i + 8); } //將strByte 轉成一個byte ,放入到huffmanCodeBytes huffmanCodeBytes[index] = (byte) Integer.parseInt(strByte, 2); index++; } return huffmanCodeBytes; } //生成赫夫曼樹對應的赫夫曼編碼表 //思路: //1. 將赫夫曼編碼表存放在Map<Byte,String>,形式如32->01,97->100... static Map<Byte, String> huffmanCodes = new HashMap<>(); //2. 在生成赫夫曼編碼表時,需要拼接路徑,定義一個StringBuilder 存儲某個葉子節點的路徑 static StringBuilder stringBuilder = new StringBuilder(); /** * 將傳入的node 節點的所有葉子的赫夫曼編碼得到,并放入huffmanCodes集合 * * @param node 傳入節點 * @param code 路徑:左子節點是0,右子節點是1 * @param stringBuilder 用于拼接路徑 */ public static void getCodes(Node node, String code, StringBuilder stringBuilder) { StringBuilder stringBuilder2 = new StringBuilder(stringBuilder); stringBuilder2.append(code); if (node != null) { //判斷當前node 是葉子節點還是非葉子節點 if (node.data == null) {//非葉子節點 //向左遞歸處理 getCodes(node.left, "0", stringBuilder2); //向右遞歸處理 getCodes(node.right, "1", stringBuilder2); } else {//葉子節點 huffmanCodes.put(node.data, stringBuilder2.toString()); } } } //前序遍歷 public static void preOrder(Node root) { if (root != null) { root.preOrder(); } else { System.out.println("赫夫曼樹不能為空~~"); } } /** * 將字節數組轉成node集合 * * @param bytes 字節數組 * @return */ public static List<Node> getNodes(byte[] bytes) { ArrayList<Node> nodes = new ArrayList<>(); //存儲每個byte出現的次數 Map<Byte, Integer> counts = new HashMap<>(); for (byte b : bytes) { counts.merge(b, 1, (a, b1) -> a + b1); } //把每個鍵值對轉成一個node對象,并加入到nodes 集合 counts.forEach((k, v) -> nodes.add(new Node(k, v))); return nodes; } /** * 生成赫夫曼樹 * @param nodes 傳入的節點 * @return */ public static Node createHufffmanTree(List<Node> nodes) { while (nodes.size() > 1) { //排序,從小到大 Collections.sort(nodes); //(1)取出權值最小的節點(二叉樹) Node leftNode = nodes.get(0); //(2) 取出權值第二小的節點(二叉樹) Node rightNode = nodes.get(1); //(3) 構建一顆新的二叉樹 Node parent = new Node(null, leftNode.weight + rightNode.weight); parent.left = leftNode; parent.right = rightNode; //(4) 從ArrayList中刪除處理過的二叉樹 nodes.remove(leftNode); nodes.remove(rightNode); //(5) 將parent加入nodes nodes.add(parent); } //nodes 的最后一個就是赫夫曼樹的root節點 return nodes.get(0); } } //創建Node,帶數據和權值 class Node implements Comparable<Node> { //存放數據本身,比如'a'=>'97',' ' =>'32' Byte data; //權值,表示字符出現的次數 int weight; Node left; Node right; public Node(Byte data, int weight) { this.data = data; this.weight = weight; } public void preOrder() { System.out.println(this); if (this.left != null) { this.left.preOrder(); } if (this.right != null) { this.right.preOrder(); } } @Override public int compareTo(Node o) { //從小到大排序 return this.weight - o.weight; } @Override public String toString() { return "Node{" + "data=" + data + ", weight=" + weight + '}'; } }如果文件本身就經過壓縮處理的,那么使用赫夫曼編碼再壓縮效率不會有明顯的變化,比如視頻,ppt等文件。
赫夫曼編碼是按字節來處理的,因此可以處理所有的文件(二進制文件,文本文件)
如果一個文件中的內容,重復的數據不多,壓縮效果也不會明顯。
“什么是赫夫曼編碼”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。