您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
小編給大家分享一下怎么利用python進行數值分析,希望大家閱讀完這篇文章之后都有所收獲,下面讓我們一起去探討吧!
噪聲是在擬合過程中常用的干擾手段,常用的噪聲:
1.統一分布 U(a,b)
f ( x ) = { 1 i f a ≤ x < b 0 o t h e r f(x)=\begin{cases}\begin{aligned}1&\quad if\quad a\le x<b \\ 0&\quad other\end{aligned}\end{cases} f(x)={10ifa≤x<bother
import numpy as np x=np.random.uniform(a,b,100) #產生長度為100的U(a,b)
2.正態分布N( μ \mu μ, σ 2 \sigma^2 σ2)
import numpy as np x=np.random.normal(mu, sig, 100) #產生長度為100的N(mu, sqart(sig))
def spline_fit(): size = 20 x = np.linspace(-10, 10, size) y = np.sin(x) + np.random.normal(0, 0.1, size) y2 = [0] * len(y) # for y_i in y: pp.plot(x, y) cs = CubicSpline(x, y) x2 = x = np.linspace(-10, 10, size * 100) pp.plot(x2, cs(x2)) pp.show()
def least_square(): f = lambda p0, xx: p0[0] * np.sin(xx * p0[1]) + p0[2] LEN = 100 x = np.linspace(-1, 1, LEN) y = x ** 2 + 5 # 默認情況,param只會返回求得的參數和返回的錯誤碼,1-4為成功,5-8為失敗,如果想輸出更多參數,可以指定full_out=1,可以看到出錯原因和其他參數 param = leastsq(lambda p0, xx, yy: f(p0, xx) - yy, (1, 1, 1), args=(x, y)) #初值的選擇比較重要,如果選取不當,容易陷入局部最優 print(param) pp.scatter(x, y) p0 = param[0] pp.plot(x, f(p0, x)) pp.show()
最小二乘的初值選取非常重要,以下是三份完全相同的數據,雖然最后都收斂了,但是初值不同,得到了完全不同的擬合結果
初值為 ( 1 , 2 , 1 ) (1,2,1) (1,2,1)
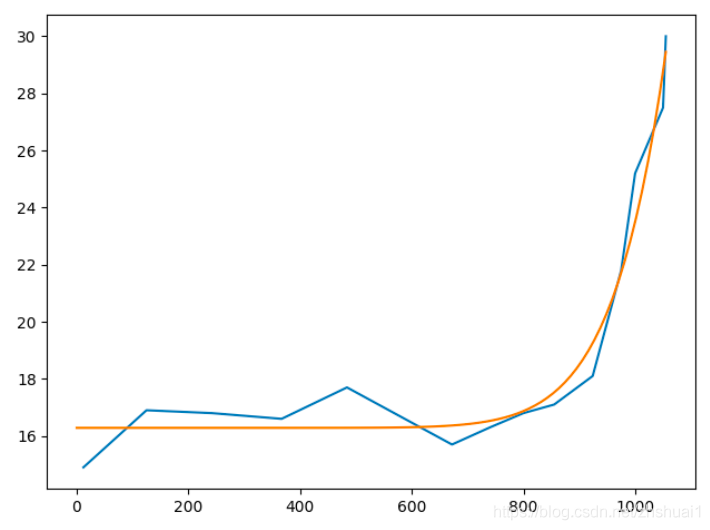
初值為 ( 1 , 1 , 1 ) (1,1,1) (1,1,1)
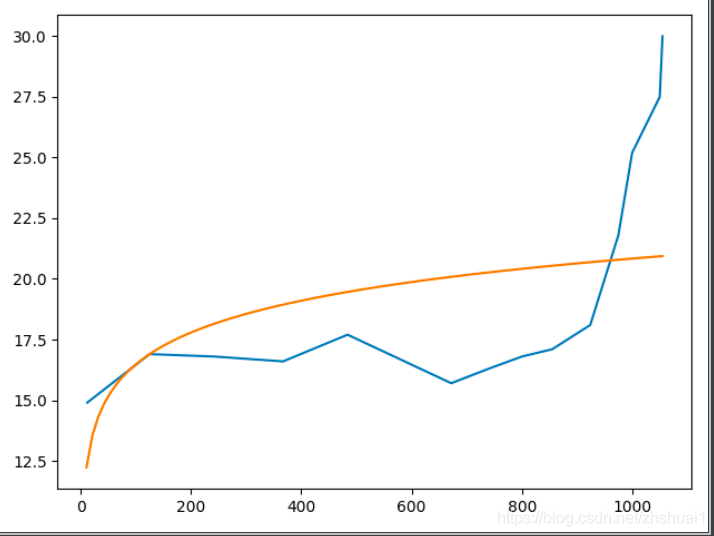
初值為 ( 10 , 10 , 1 ) (10,10,1) (10,10,1)
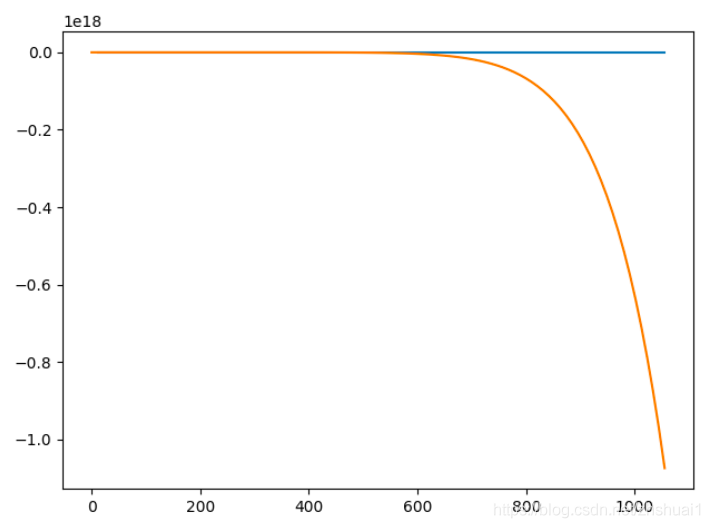
def lagrange()
from scipy.optimize import minimize
import numpy as np
e = 1e-10
fun = lambda x: 8 * (x[0] * x[1] * x[2]) # f(x,y,z) =8 *x*y*z
cons = ({'type': 'eq', 'fun': lambda x: x[0] ** 2 + x[1] ** 2 + x[2] ** 2 - 1}, # x^2 + y^2 + z^2=1
{'type': 'ineq', 'fun': lambda x: x[0] - e}, # x>=e等價于 x > 0
{'type': 'ineq', 'fun': lambda x: x[1] - e},
{'type': 'ineq', 'fun': lambda x: x[2] - e}
)
x0 = np.array((1.0, 1.0, 1.0)) # 設置初始值
res = minimize(fun, x0, method='SLSQP', constraints=cons)
print('最大值:', res.fun)
print('最優解:', res.x)
print('迭代終止是否成功:', res.success)
print('迭代終止原因:', res.message)看完了這篇文章,相信你對“怎么利用python進行數值分析”有了一定的了解,如果想了解更多相關知識,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。