您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關python如何實現高斯模糊的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
高斯模糊是一種常見的模糊技術,相關知識點有:高斯函數、二維卷積。
一維(連續變量)高斯函數形式如下,高斯函數又稱“正態分布函數”:
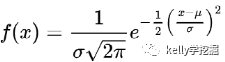
μ是分布函數的均值(或者期望),sigma是標準差。
一維高斯分布函數的圖形:
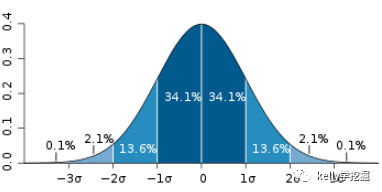
從圖可知,以x=0為中心,x取值距離中心越近,概率密度函數值越大,距離中心越遠,密度函數值越小。
二維高斯分布函數的形式:

特別說明,當變量x和y相互獨立時,則相關系數ρ=0,二維高斯分布函數可以簡化為:
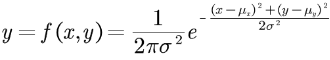
二維高斯分布函數的圖形:
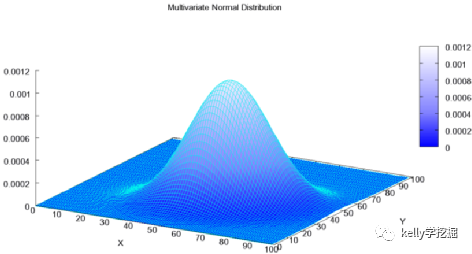
對于一維高斯分布,函數中心是平面上的一個點;而對于二維高斯分布,函數中心是一個三維立體空間上的一個點,即上圖中山峰的最頂端處的點。
高斯模糊本質上一種數據平滑技術,可以用于一維、二維甚至多維空間。數據經高斯模糊處理之后,數據會趨向于周邊鄰近的其他數據,導致各個數據“趨同”。
在圖像領域,各個位置的像素值使用“周邊鄰居像素點加權平均”重新賦值。對于每個像素點,由于計算時均以當前像素點為中心,所以均值μ=0。使用時有2個超參數需要設置:高斯核大小和高斯函數標準差σ。高斯核大小表示“影響當前點的最大鄰域范圍”,而標準差表示“鄰域中的其他像素點對當前點的影響力”。
從下而上觀察下圖各個函數圖像,各個函數的均值相同,而方差逐步減小。
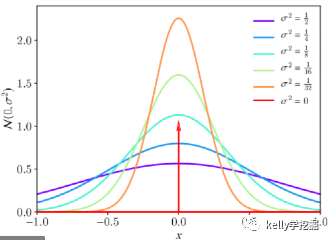
方差衡量數據的分散程度,方差越大,數據越分散,圖形就越扁平,數據的集中趨勢越弱,應用到高斯模糊中方差越大圖形越模糊。
(1)如何計算高斯卷積核
3×3大小的高斯卷積核的計算示意圖
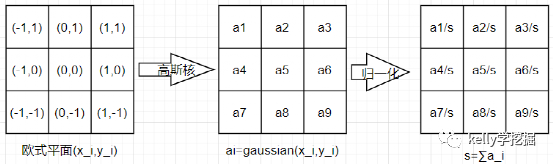
直接計算二維高斯函數值后,卷積核的各個位置取值(截圖自pycharm的debug):
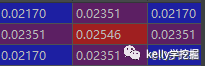
卷積核歸一化后的各個位置取值(截圖自pycharm的debug):
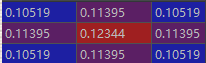
高斯卷積核的python代碼:
def gaussian_kernel(self): kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float) radius = self.kernel_size//2 for y in range(-radius, radius + 1): # [-r, r] for x in range(-radius, radius + 1): # 二維高斯函數 v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2)) kernel[y + radius, x + radius] = v # 高斯函數的x和y值 vs 高斯核的下標值 kernel2 = kernel / np.sum(kernel) return kernel2
(2)如何在二維圖像上進行卷積
對于二維矩陣,卷積時卷積核從左向右、從上而下的滑動,對應位置求加權和。一般圖像是RGB三通道,需要逐個通道卷積,每個通道是一個二維矩陣。灰度圖只有一個通道,直接卷積即可。
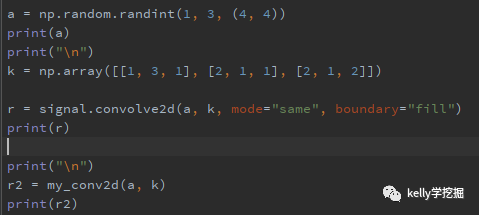
自行實現的二維離散卷積的python代碼:
def my_conv2d(inputs: np.ndarray, kernel: np.ndarray): # 計算需要填充的行列數目,這里假定mode為“same” # 一般卷積核的hw都是奇數,這里實現方式也是基于奇數尺寸的卷積核 h, w = inputs.shape kernel = kernel[::-1, ...][..., ::-1] # 卷積的定義,必須旋轉180度 h2, w1 = kernel.shape h_pad = (h2 - 1) // 2 w_pad = (w1 - 1) // 2 inputs = np.pad(inputs, pad_width=[(h_pad, h_pad), (w_pad, w_pad)], mode="constant", constant_values=0) outputs = np.zeros(shape=(h, w)) for i in range(h): # 行號 for j in range(w): # 列號 outputs[i, j] = np.sum(np.multiply(inputs[i: i + h2, j: j + w1], kernel)) return outputs
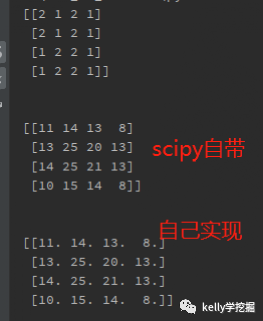
scipy中已經提供二維卷積函數scipy.signal.convolve2d,可以直接調用,下圖是和自行實現的對比效果。
運行之后結果一致,驗證自行實現的二維卷積正確。
補充:scipy.signal.convolve2d的參數說明
in1:輸入矩陣
in2:卷積核
mode:指示輸出矩陣的尺寸,full代表完全離散線性卷積, valid代表輸出尺寸等于輸入尺寸-卷積核+1, same代表輸出尺寸與輸入尺寸一致。
boundary:需要填充時邊界填充方式,fill代表使用常量值填充, wrap代表循環方式填充, symm代表以四周邊為對稱軸對稱填充。
fillvalue:常量填充時的填充值
完整的python代碼
class GaussianBlur(object):
def __init__(self, kernel_size=3, sigma=1.5):
self.kernel_size = kernel_size
self.sigma = sigma
self.kernel = self.gaussian_kernel()
def gaussian_kernel(self):
kernel = np.zeros(shape=(self.kernel_size, self.kernel_size), dtype=np.float)
radius = self.kernel_size//2
for y in range(-radius, radius + 1): # [-r, r]
for x in range(-radius, radius + 1):
# 二維高斯函數
v = 1.0 / (2 * np.pi * self.sigma ** 2) * np.exp(-1.0 / (2 * self.sigma ** 2) * (x ** 2 + y ** 2))
kernel[y + radius, x + radius] = v # 高斯函數的x和y值 vs 高斯核的下標值
kernel2 = kernel / np.sum(kernel)
return kernel2
def filter(self, img: Image.Image):
img_arr = np.array(img)
if len(img_arr.shape) == 2:
new_arr = signal.convolve2d(img_arr, self.kernel, mode="same", boundary="symm")
else:
h, w, c = img_arr.shape
new_arr = np.zeros(shape=(h, w, c), dtype=np.float)
for i in range(c):
new_arr[..., i] = signal.convolve2d(img_arr[..., i], self.kernel, mode="same", boundary="symm")
new_arr = np.array(new_arr, dtype=np.uint8)
return Image.fromarray(new_arr)
def main():
img = Image.open("Jeep-cd.jpg").convert("RGB")
img2 = GaussianBlur(sigma=2.5).filter(img)
plt.subplot(1, 2, 1)
plt.imshow(img)
plt.subplot(1, 2, 2)
plt.imshow(img2)
# dpi參數維持圖片的清晰度
plt.savefig("gaussian.jpg", dpi=500)
plt.show()
pass代碼運行效果,發現經高斯模糊處理之后,圖片發生明顯模糊。


1、云計算,典型應用OpenStack。2、WEB前端開發,眾多大型網站均為Python開發。3.人工智能應用,基于大數據分析和深度學習而發展出來的人工智能本質上已經無法離開python。4、系統運維工程項目,自動化運維的標配就是python+Django/flask。5、金融理財分析,量化交易,金融分析。6、大數據分析。
感謝各位的閱讀!關于“python如何實現高斯模糊”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。