您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了使用matplotlib怎么繪制一個正余弦曲線圖,此處通過實例代碼給大家介紹的非常詳細,對大家的學習或工作具有一定的參考價值,需要的朋友可以參考下:
matplotlib numpy
matplotlib 是我們本章需要的庫
numpy 是我們數據分析處理的常見庫,在機器學習時也會經常用到。
一步一步來了
下面展示一些 內聯代碼片。
第一步
#1:用到的方法及參數 # linspace(start, stop, num=50, endpoint=True, # retstep=False, dtype=None) # 相關參數的說明 # 指定在start到stop均分數值 # start:不可省略 # stop:有時包含有時不包含,根據endpoint來選擇,默認包含 # num:指定均分的數量,默認為50 # endpoint:布爾值,可選,默認為True。包含stop就True,不包含就# False # retstep : 布爾值,可選,默認為False。如果為True,返回值和步長 # dtype : 輸出數據類型,可選。如果不指定,則根據前面參數的數據類型 # 2:np.plot(x,y.color.lw,label,ls,mk,mec,mfc) # 其中X由所有輸入點坐標的x值組成,Y是由與X中包含的x對應的y所組 # 成的向量 # color 指定線條的顏色 # lw指定線條的寬度 # lw指定線條的樣式,默認為實現 # mk可以指定數據標識符 # ms可以指定標識符的大小 # mec可以指定標識符的邊界色彩 # mfc標識符內部填充顏色
import matplotlib.pyplot as plt import numpy as np #用于正常顯示中文標簽 plt.rcParams['font.sans-serif']=['SimHei'] # 用于正常顯示符號 plt.rcParams['axes.unicode_minus']=False x = np.linspace(-np.pi,np.pi,256,endpoint = 256) sin,cos = np.sin(x),np.cos(x) #繪制,并設置相關的參數,這里標簽還不會顯示出來,因為還沒有 #添加圖例,具體往下面看 plt.plot(x,sin,color = 'blue',lw=2.5,label = '正弦sin',mec='red') plt.plot(x,cos,color = 'red',lw = 2.5,label = '余弦cos()') plt.show() #顯示
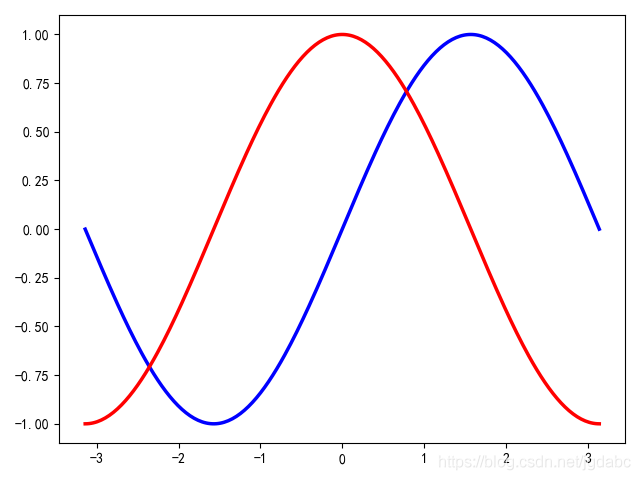
第二步
#用到的方法及參數 # plt.xlim(xmin, xmax) # xmin:x軸上的最小值 # xmax:x軸上的最大值 #plt.ylim() 與上一樣的道理 #具體如何使用,可以看下面的實例代碼
plt.xlim(x.min()*1.5,x.max()*1.5) #將x軸拉伸1.5倍 plt.ylim(cos.min()*1.5,cos.max()*1.5) # 將y軸拉伸1.5倍 plt.show()
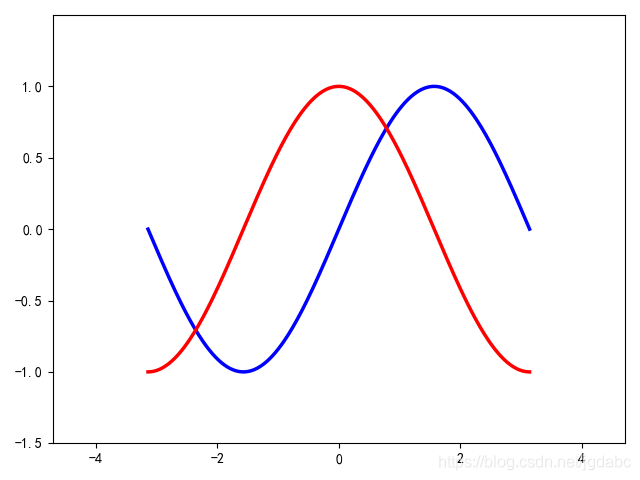
第三步
#用到的方法與參數
# plt.xticks([],[])
# plt.yticks([],[])
# plt.title('',color,color,..) #設置標題,里面的相關參數可以# 指定
# plt.text(備注內容x軸的坐標,備注內容y軸的坐標 ,'備注內容',fontsize,color,..) #給右下角添加備注
#想說的說這里面有連個參數,分別以列表的形式展示。
現在只需要介紹是用來設置坐標刻度的。其中第二個參數列表
是用來轉義的。具體實例如下。下面展示一些 內聯代碼片。
在x軸的刻度上,我們需要我們需要按照規則的正余弦刻度來,而不是簡單的實數,我們需要圓周率。因此在plt.xticks([],[])的第二個列表參數上需要轉義。
#這里的r'$代表開始,$代表結尾,\代表轉義,\pi代表圓周率的意思,r代表原始字符串。因此可以一一對應下來的。
plt.xticks([-np.pi,-np.pi/2,0,np.pi/2,np.pi],
[r'$-\pi$',r'$-\pi/2$',r'$0$',r'$\pi/2$',r'$\pi$'])
plt.yticks([-1,0,1])
plt.title("繪圖正余弦函數曲線圖",fontsize = 16,color ='green')
#給圖片右下角添加備注標簽
plt.text(+2.2,-1.4,"by:jgdabc",fontsize=16,color = 'purple')
plt.show()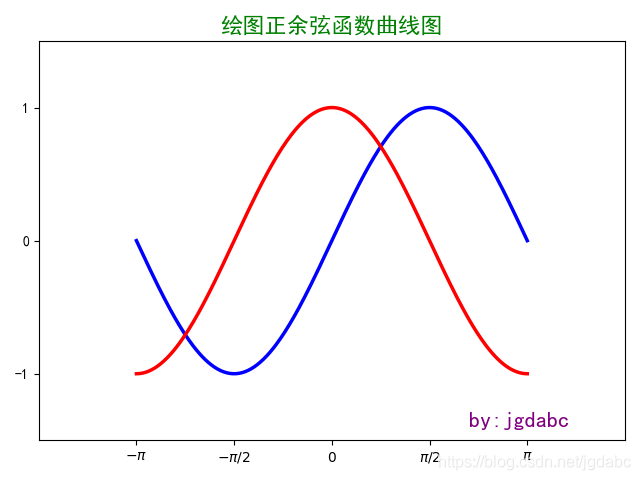
第四步:
用到的方法及參數:
plt.gca()#這個方法有點東西。
我要簡單的去理解,Python庫太繁雜了。有點頭大。
plt.gca(),可以獲得axes對象
什么又是axes對象?
在matplotlib中,整個圖表為一個figure對象。每個figure
對象中可以包含一個或多個axes,而axes為坐標軸。每個axes
對象都是一個擁有自己坐標系統的繪圖區域。我們可以理解為通
過這個方法我們可以獲得axes對象,而通過這個對象可以幫助我們
方便的操作坐標軸,ok。具體操作看實例吧!
#我相信能看懂英文的不看注釋也可以看懂
ax = plt.gca() #獲取Axes對象
ax.spines['right'].set_color('none') #隱藏右邊界
ax.spines['top'].set_color('none')#隱藏上邊界
ax.xaxis.set_ticks_position('bottom') #x軸坐標刻度設置在坐標下面
ax.spines['bottom'].set_position(('data',0))#將x坐標軸平移經過(0,0)的位置
ax.yaxis.set_ticks_position('left')#將y軸坐標刻度設置在坐標軸左側
ax.spines['left'].set_position(('data',0))#將y軸坐標軸平移到(0,0)位置
plt.show()兄弟們是不是有點像了,還不夠。
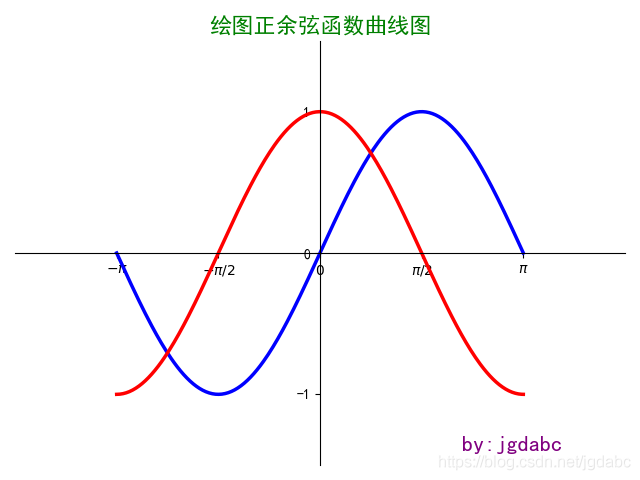
第五步:
用到的方法及參數:
plt.legend()
添加圖例
這樣才會把我上述label的內容顯示出來。
plt.legend(loc ='upper left',fontsize=12) plt.show()
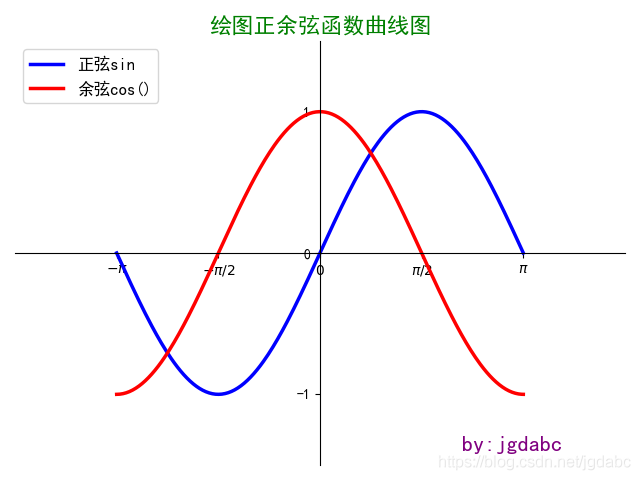
第六步
注意第六步我們要描點,并畫線
用到的方法及參數
plt.plot() # 這個前面已經有說明,不再贅述,這里我們
要加一個參數linewidth指定,將其變為虛線
plt.scatter() #用來繪制兩個點的位置
plt.annotate #用來添加注釋文字,具體解釋我們在實例代碼中說明
```javascript
t1 = 2*np.pi/3 #取一個x軸坐標點
t2 = -np.pi # 取第二個坐標點
#根據畫線,第一個列表是x軸坐標值,第二個列表是y軸坐標值
plt.plot([t1,t1],[0,np.sin(t1)],color = 'b',linewidth = 1.5,linestyle = '--')
#畫線
plt.plot([t2,t2],[0,np.cos(t2)],color ='r',linewidth=1.5,line)
#標注兩個點的位置(繪制散點圖的方法)
plt.scatter([t1,],[np.sin(t1),],50,color = 'b') #50為指定的大小
#為圖表添加注釋
plt.scatter([t2,],[np.cos(2),],50,color = 'r')
plt.annotate( r'$\sin(\frac{2\pi}{3}=\frac{\sqrt{3}}{2}$)',
xy = (t1,np.sin(t1)), #點的位置
xycoords = 'data', #注釋文字的偏移量
xytext = (+10,+30), #文字離點的橫縱距離
textcoords = 'offset points',
fontsize =14,#注釋的大小
arrowprops = dict(arrowstyle = '->',connectionstyle = 'arc3,rad=.2')#箭頭指向的彎曲度
)
plt.annotate(r'$\cos(-\pi)=-1$',
xy = (t2,np.cos(t2)),
xycoords = 'data', #注釋文字的偏移量
xytext = (0 ,-40), # 文字離點的橫縱距離
textcoords = 'offset points',
fontsize = 14,#注釋的大小
arrowprops = dict(arrowstyle = '->',connectionstyle='arc3,rad=.2')
) #點的位置
plt.show()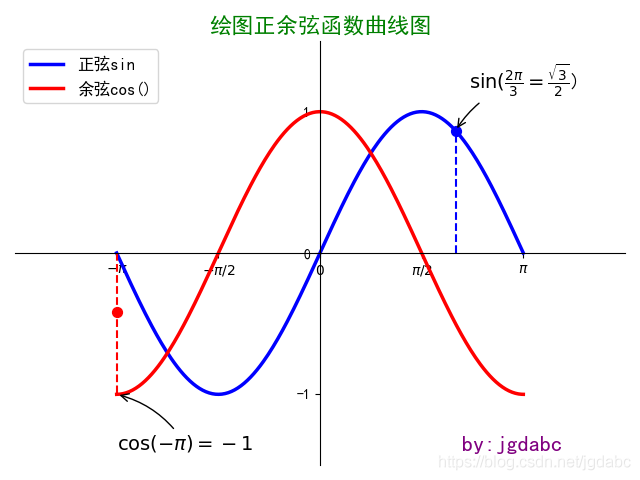
第七步:我想設置一下x軸和y軸的字體,一提到軸,就用ax.
我們直接上代碼去解釋
#遍歷獲取x軸和y軸的刻度,并設置字體
for label in ax.get_xticklabels() + ax.get_yticklabels() :
label.set_fontsize(18)
label.set_bbox(dict(facecolor = 'r',edgecolor='g',alpha=0.5))#alpha代表透明度
#繪制填充區域
plt.fill_between(x,np.abs(x)<0.5,sin,sin>0.5,color='g',alpha =0.8)
plt.fill_between(x,cos,where = (-2.5<x)&(x<-0.5),color = 'purple')
plt.grid() #繪制網格線
plt.savefig("D:\python學習數據可視化matplot學習.png",dpi = 300)保存圖片
plt.show()注意這里保存一定要先保存,后show。
最終效果

給大家完整代碼
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False
x = np.linspace(-np.pi,np.pi,256,endpoint=256)
sin,cos = np.sin(x),np.cos(x)
plt.plot(x,sin,color = 'blue',lw=2.5,label = '正弦sin',mec='red')
plt.plot(x,cos,color = 'red',lw = 2.5,label = '余弦cos()')
plt.xlim(x.min()*1.5,x.max()*1.5)
plt.ylim(cos.min()*1.5,cos.max()*1.5)
plt.xticks([-np.pi,-np.pi/2,0,np.pi/2,np.pi],[r'$-\pi$',r'$-\pi/2$',r'$0$',r'$\pi/2$',r'$\pi$'])
plt.yticks([-1,0,1])
plt.title("繪圖正余弦函數曲線圖",fontsize = 16,color ='green')
plt.text(+2.2,-1.4,"by:jgdabc",fontsize=16,color = 'purple')
ax = plt.gca()
ax.spines['right'].set_color('none')
ax.spines['top'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.legend(loc ='upper left',fontsize=12)
t1 = 2*np.pi/3
t2 = -np.pi
plt.plot([t1,t1],[0,np.sin(t1)],color = 'b',linewidth = 1.5,linestyle = '--')
plt.plot([t2,t2],[0,np.cos(t2)],color ='r',linewidth=1.5,line)
plt.scatter([t1,],[np.sin(t1),],50,color = 'b')
plt.scatter([t2,],[np.cos(2),],50,color = 'r')
plt.annotate( r'$\sin(\frac{2\pi}{3}=\frac{\sqrt{3}}{2}$)',
xy = (t1,np.sin(t1)),
xycoords = 'data',
xytext = (+10,+30),
textcoords = 'offset points',
fontsize =14,
arrowprops = dict(arrowstyle= '->',connectionstyle = 'arc3,rad=.2')#箭頭指向的彎曲度
)
plt.annotate(r'$\cos(-\pi)=-1$',
xy = (t2,np.cos(t2)),
xycoords = 'data',
xytext = (0 ,-40),
textcoords = 'offset points',
fontsize = 14,
arrowprops = dict(arrowstyle = '->',connectionstyle='arc3,rad=.2')
)
for label in ax.get_xticklabels() + ax.get_yticklabels() :
label.set_fontsize(18)
label.set_bbox(dict(facecolor = 'r',edgecolor='g',alpha=0.5))
plt.fill_between(x,np.abs(x)<0.5,sin,sin>0.5,color='g',alpha =0.8)
plt.fill_between(x,cos,where = (-2.5<x)&(x<-0.5),color = 'purple')
plt.grid()
plt.savefig("D:\python學習數據可視化matplot學習.png",dpi = 300)
plt.show()到此這篇關于使用matplotlib怎么繪制一個正余弦曲線圖的文章就介紹到這了,更多相關內容請搜索億速云以前的文章或繼續瀏覽下面的相關文章希望大家以后多多支持億速云!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。