溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
本篇文章為大家展示了反向傳播算法如何在python項目中實現,內容簡明扼要并且容易理解,絕對能使你眼前一亮,通過這篇文章的詳細介紹希望你能有所收獲。
反向傳播的目的是計算成本函數C對網絡中任意w或b的偏導數。一旦我們有了這些偏導數,我們將通過一些常數 α的乘積和該數量相對于成本函數的偏導數來更新網絡中的權重和偏差。這是流行的梯度下降算法。而偏導數給出了最大上升的方向。因此,關于反向傳播算法,我們繼續查看下文。
我們向相反的方向邁出了一小步——最大下降的方向,也就是將我們帶到成本函數的局部最小值的方向。
圖示演示:
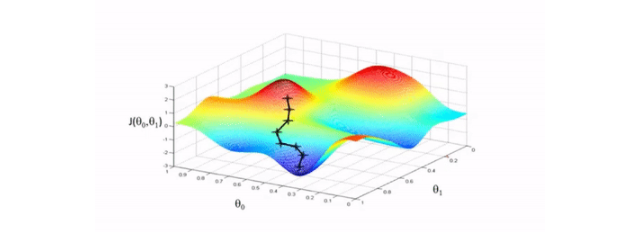
反向傳播算法中Sigmoid函數代碼演示:
# 實現 sigmoid 函數 return 1 / (1 + np.exp(-x)) def sigmoid_derivative(x): # sigmoid 導數的計算 return sigmoid(x)*(1-sigmoid(x))
反向傳播算法中ReLU 函數導數函數代碼演示:
def relu_derivative(x): # ReLU 函數的導數 d = np.array(x, copy=True) # 用于保存梯度的張量 d[x < 0] = 0 # 元素為負的導數為 0 d[x >= 0] = 1 # 元素為正的導數為 1 return d
實例擴展:
BP反向傳播算法Python簡單實現
import numpy as np
# "pd" 偏導
def sigmoid(x):
return 1 / (1 + np.exp(-x))
def sigmoidDerivationx(y):
return y * (1 - y)
if __name__ == "__main__":
#初始化
bias = [0.35, 0.60]
weight = [0.15, 0.2, 0.25, 0.3, 0.4, 0.45, 0.5, 0.55]
output_layer_weights = [0.4, 0.45, 0.5, 0.55]
i1 = 0.05
i2 = 0.10
target1 = 0.01
target2 = 0.99
alpha = 0.5 #學習速率
numIter = 10000 #迭代次數
for i in range(numIter):
#正向傳播
neth2 = i1*weight[1-1] + i2*weight[2-1] + bias[0]
neth3 = i1*weight[3-1] + i2*weight[4-1] + bias[0]
outh2 = sigmoid(neth2)
outh3 = sigmoid(neth3)
neto1 = outh2*weight[5-1] + outh3*weight[6-1] + bias[1]
neto2 = outh3*weight[7-1] + outh3*weight[8-1] + bias[1]
outo1 = sigmoid(neto1)
outo2 = sigmoid(neto2)
print(str(i) + ", target1 : " + str(target1-outo1) + ", target2 : " + str(target2-outo2))
if i == numIter-1:
print("lastst result : " + str(outo1) + " " + str(outo2))
#反向傳播
#計算w5-w8(輸出層權重)的誤差
pdEOuto1 = - (target1 - outo1)
pdOuto1Neto1 = sigmoidDerivationx(outo1)
pdNeto1W5 = outh2
pdEW5 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W5
pdNeto1W6 = outh3
pdEW6 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W6
pdEOuto2 = - (target2 - outo2)
pdOuto2Neto2 = sigmoidDerivationx(outo2)
pdNeto1W7 = outh2
pdEW7 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W7
pdNeto1W8 = outh3
pdEW8 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W8
# 計算w1-w4(輸出層權重)的誤差
pdEOuto1 = - (target1 - outo1) #之前算過
pdEOuto2 = - (target2 - outo2) #之前算過
pdOuto1Neto1 = sigmoidDerivationx(outo1) #之前算過
pdOuto2Neto2 = sigmoidDerivationx(outo2) #之前算過
pdNeto1Outh2 = weight[5-1]
pdNeto2Outh3 = weight[7-1]
pdEOuth2 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh2 + pdEOuto2 * pdOuto2Neto2 * pdNeto1Outh2
pdOuth2Neth2 = sigmoidDerivationx(outh2)
pdNeth2W1 = i1
pdNeth2W2 = i2
pdEW1 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W1
pdEW2 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W2
pdNeto1Outh3 = weight[6-1]
pdNeto2Outh3 = weight[8-1]
pdOuth3Neth3 = sigmoidDerivationx(outh3)
pdNeth3W3 = i1
pdNeth3W4 = i2
pdEOuth3 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh3 + pdEOuto2 * pdOuto2Neto2 * pdNeto2Outh3
pdEW3 = pdEOuth3 * pdOuth3Neth3 * pdNeth3W3
pdEW4 = pdEOuth3 * pdOuth3Neth3 * pdNeth3W4
#權重更新
weight[1-1] = weight[1-1] - alpha * pdEW1
weight[2-1] = weight[2-1] - alpha * pdEW2
weight[3-1] = weight[3-1] - alpha * pdEW3
weight[4-1] = weight[4-1] - alpha * pdEW4
weight[5-1] = weight[5-1] - alpha * pdEW5
weight[6-1] = weight[6-1] - alpha * pdEW6
weight[7-1] = weight[7-1] - alpha * pdEW7
weight[8-1] = weight[8-1] - alpha * pdEW8
# print(weight[1-1])
# print(weight[2-1])
# print(weight[3-1])
# print(weight[4-1])
# print(weight[5-1])
# print(weight[6-1])
# print(weight[7-1])
# print(weight[8-1])上述內容就是反向傳播算法如何在python項目中實現,你們學到知識或技能了嗎?如果還想學到更多技能或者豐富自己的知識儲備,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。