您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
了解MySQL索引要用B+tree的原因?這個問題可能是我們日常學習或工作經常見到的。希望通過這個問題能讓你收獲頗深。下面是小編給大家帶來的參考內容,讓我們一起來看看吧!
當你現在遇到了一條慢 SQL 需要進行優化時,你第一時間能想到的優化手段是什么?
大部分人第一反應可能都是添加索引,在大多數情況下面,索引能夠將一條 SQL 語句的查詢效率提高幾個數量級。
索引的本質:用于快速查找記錄的一種數據結構。
索引的常用數據結構:
B-tree (B樹,并不叫什么B減樹)B+tree數據結構圖形化網址:https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
大家知道 select * from t where col = 88 這么一條 SQL 語句如果不走索引進行查找的話,正常地查就是全表掃描:從表的第一行記錄開始逐行找,把每一行的 col 字段的值和 88 進行對比,這明顯效率是很低的。
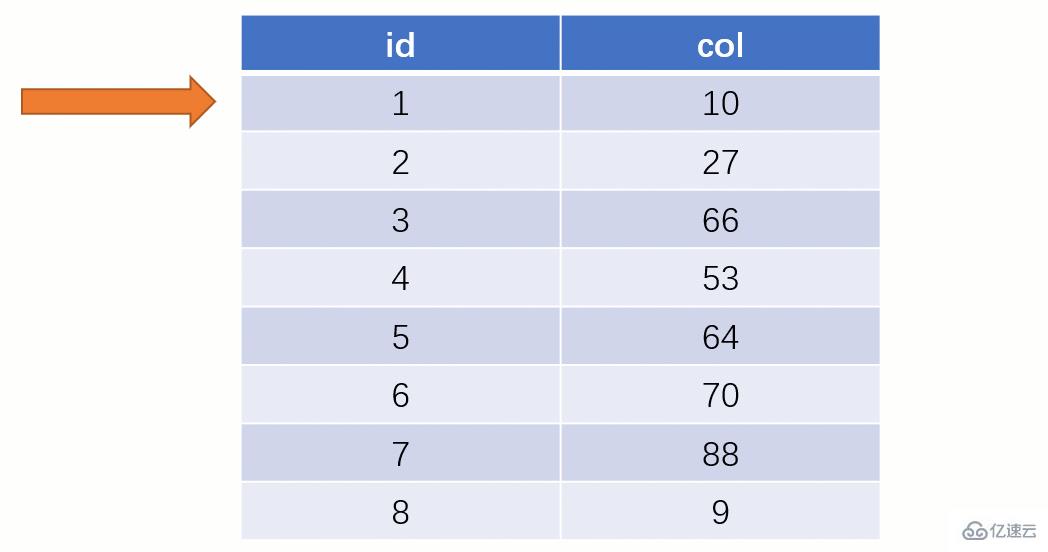
而如果走索引的話,查詢的流程就完全不一樣了(假設現在用一棵平衡二叉樹數據結構存儲我們的索引列)
此時該二叉樹的存儲結構(Key - Value):Key 就是索引字段的數據,Value 就是索引所在行的磁盤文件地址。
當最后找到了 88 的時候,就可以把它的 Value 對應的磁盤文件地址拿出來,然后就直接去磁盤上去找這一行的數據,這時候的速度就會比全表掃描要快很多。
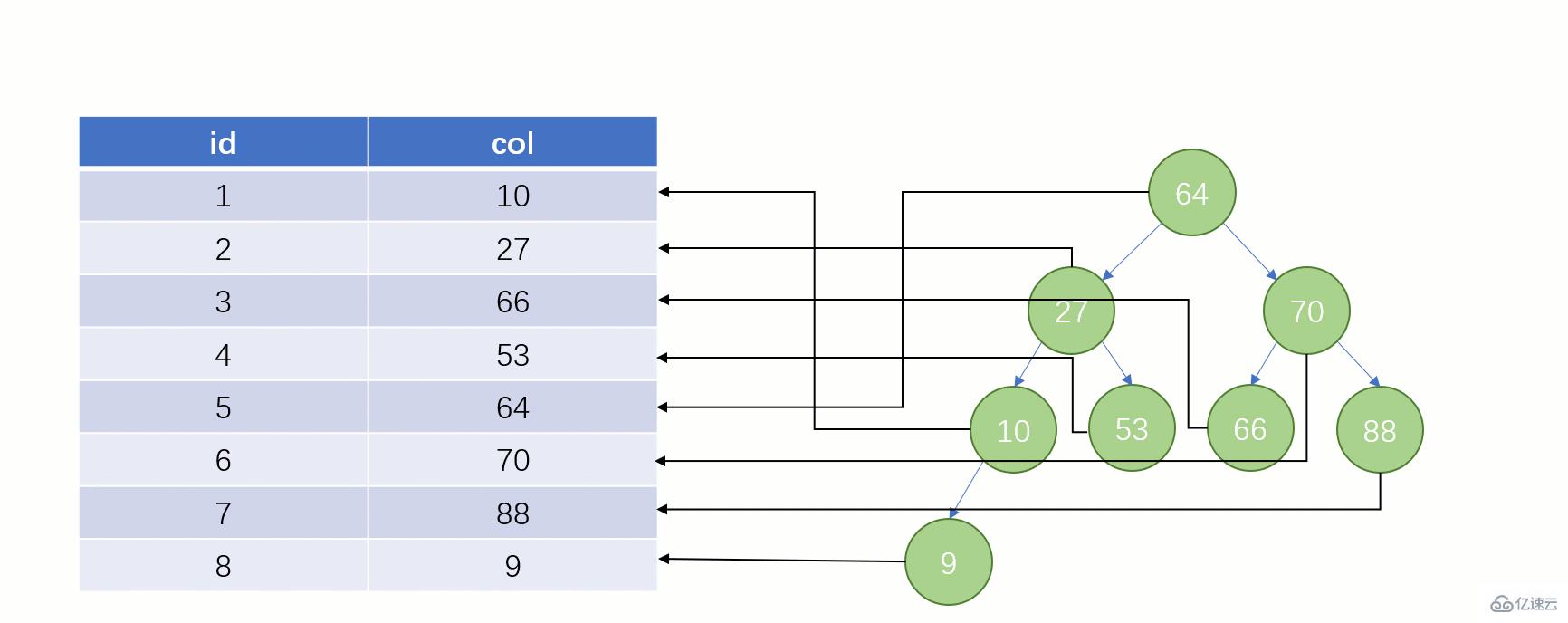
但實際上 MySQL 底層并沒有用二叉樹來存儲索引數據,是用的 B+tree(B+樹)。
假設此時用普通二叉樹記錄 id 索引列,我們在每插入一行記錄的同時還要維護二叉樹索引字段。
此時當我要找 id = 7 的那條數據時,它的查找過程如下:
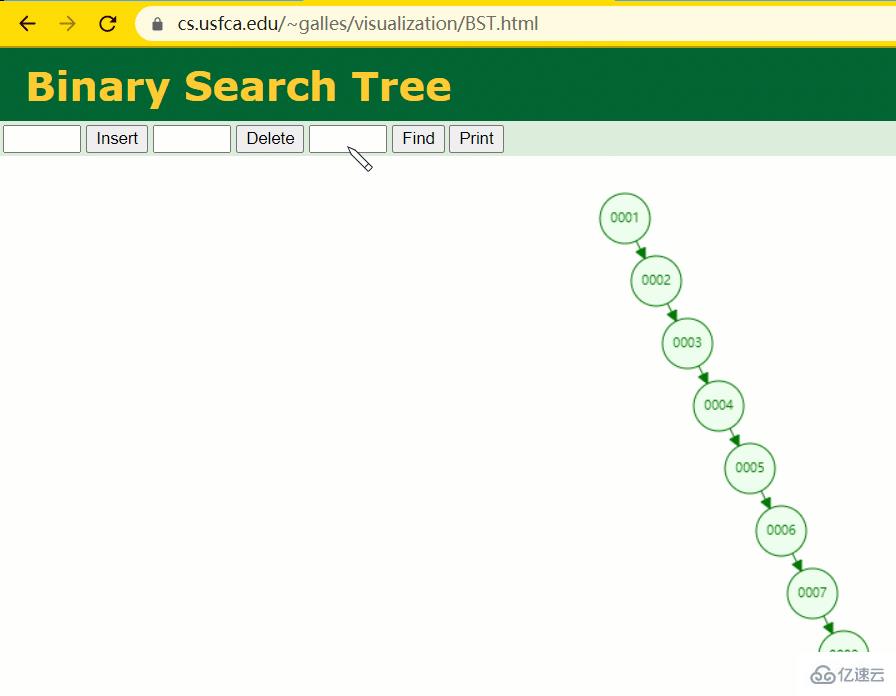
此時找 id = 7 這一行記錄時找了 7 次,和我們全表掃描也沒什么很大區別。顯而易見,二叉樹對于這種依次遞增的數據列其實是不適合作為索引的數據結構。
Hash 表:一個快速搜索的數據結構,搜索的時間復雜度 O(1)
Hash 函數:將一個任意類型的 key,可以轉換成一個 int 類型的下標
假設此時用 Hash 表記錄 id 索引列,我們在每插入一行記錄的同時還要維護 Hash 表索引字段。
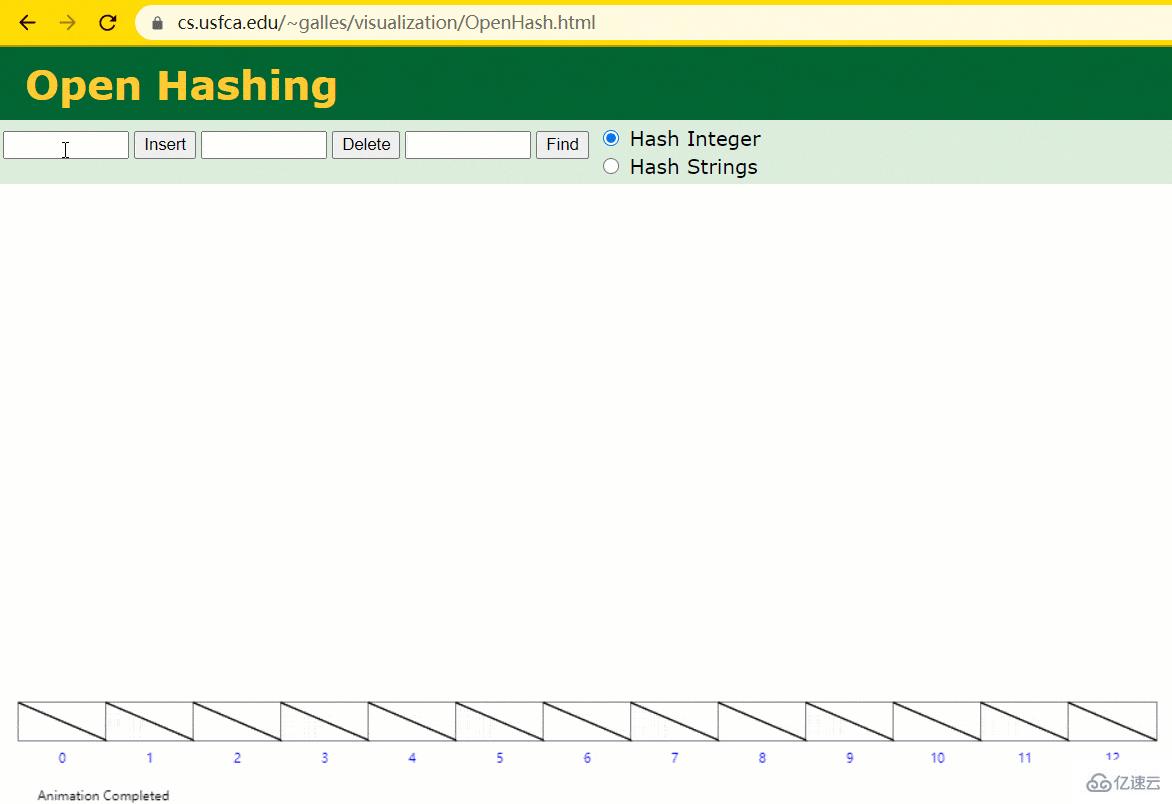
這時候開始查找 id = 7 的樹節點僅找了 1 次,效率非常高了。
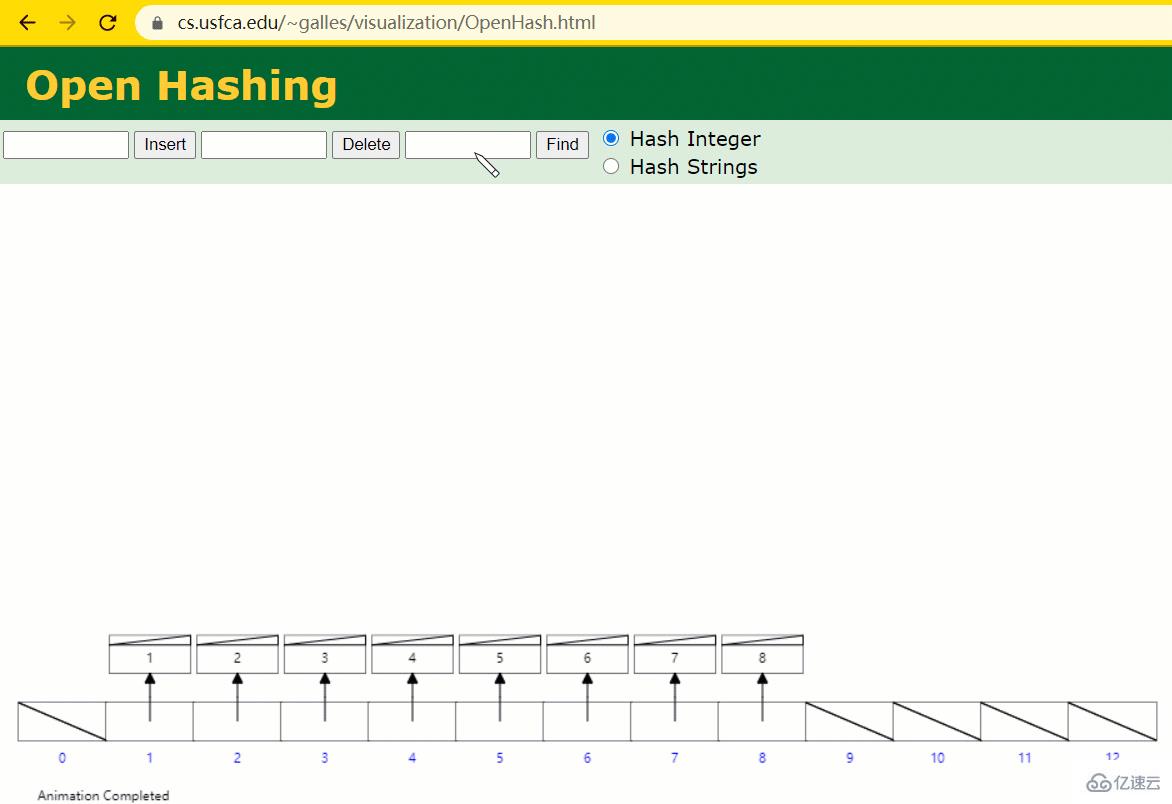
但 MySQL 的索引依然不采用能夠精準定位的Hash 表。因為它不適用于范圍查詢。
紅黑樹是一種特化的 AVL樹(平衡二叉樹),都是在進行插入和刪除操作時通過特定操作保持二叉查找樹的平衡;
若一棵二叉查找樹是紅黑樹,則它的任一子樹必為紅黑樹。
假設此時用紅黑樹記錄 id 索引列,我們在每插入一行記錄的同時還要維護紅黑樹索引字段。
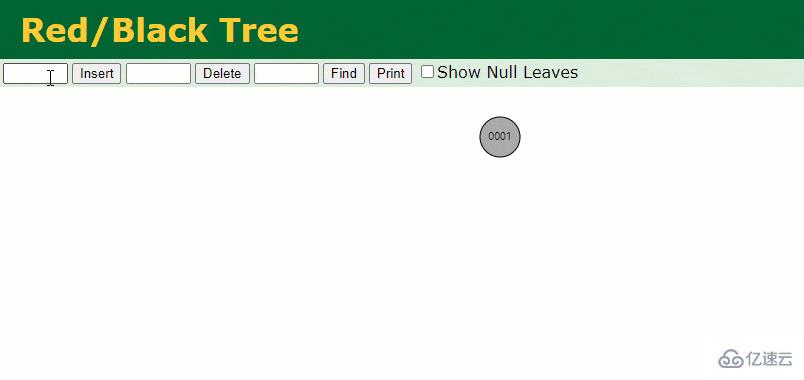
插入過程中會發現它與普通二叉樹不同的是當一棵樹的左右子樹高度差 > 1 時,它會進行自旋操作,保持樹的平衡。
這時候開始查找 id = 7 的樹節點只找了 3 次,比所謂的普通二叉樹還是要更快的。
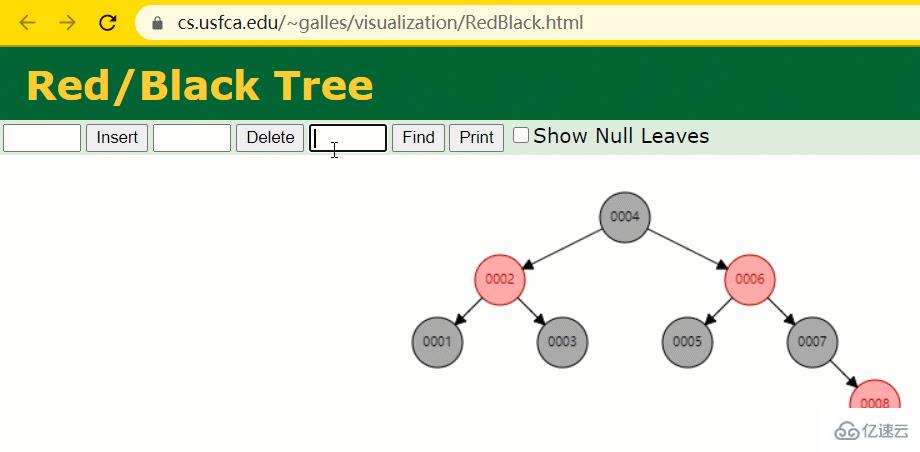
但 MySQL 的索引依然不采用能夠精確定位和范圍查詢都優秀的紅黑樹。
因為當 MySQL 數據量很大的時候,索引的體積也會很大,可能內存放不下,所以需要從磁盤上進行相關讀寫,如果樹的層級太高,則讀寫磁盤的次數(I/O交互)就會越多,性能就會越差。
紅黑樹目前的唯一不足點就是樹的高度不可控,所以現在我們的切入點就是樹的高度。
目前一個節點是只分配了一個存儲 1 個元素,如果要控制高度,我們就可以把一個節點分配的空間更大一點,讓它橫向存儲多個元素,這個時候高度就可控了。這么個改造過程,就變成了
B-tree。
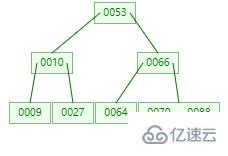
B-tree 是一顆絕對平衡的多路樹。它的結構中還有兩個概念
度(Degree):一個節點擁有的子節點(子樹)的數量。(有的地方是以度來說明
B-tree的,這里解釋一下)階(order):一個節點的子節點的最大個數。(通常用 m 表示)
關鍵字:數據索引。
一棵 m 階 B-tree 是一棵平衡的 m 路搜索樹。它可能是空樹,或者滿足以下特點:
除根節點和葉子節點外,其它每個節點至少有 ?2m? 個子節點;
?2m? 為 m / 2 然后向上取整
每個非根節點所包含的關鍵字個數 j 滿足:?2m? - 1 ≤ j ≤ m - 1;
節點的關鍵字從左到右遞增排列,有 k 個關鍵字的非葉子節點正好有 (k + 1) 個子節點;
所有的葉子結點都位于同一層。
以下摘自維基百科
魯道夫·拜爾(Rudolf Bayer)和 艾華·M·麥克雷(Ed M. McCreight)于1972年在波音研究實驗室(Boeing Research Labs)工作時發明了 B-tree,但是他們沒有解釋 B 代表什么意義(如果有的話)。
道格拉斯·科默爾(Douglas Comer)解釋說:兩位作者從來都沒解釋過 B-tree 的原始意義。我們可能覺得 balanced, broad 或 bushy 可能適合。其他人建議字母 B 代表 Boeing。源自于他的贊助,不過,看起來把 B-tree 當作 Bayer 樹更合適些。
高德納(Donald Knuth)在他1980年5月發表的題為 "CS144C classroom lecture about disk storage and B-trees" 的論文中推測了 B-tree 的名字取義,提出 B 可能意味 Boeing 或者 Bayer 的名字。
B-tree 的查找其實和二叉樹很相似:
二叉樹是每個節點上有一個關鍵字和兩個分支,B-tree 上每個節點有 k 個關鍵字和 (k + 1) 個分支。
二叉樹的查找只考慮向左還是向右走,而 B-tree 中需要由多個分支決定。
B-tree 的查找分兩步:
B-tree 通常是在磁盤上存儲的所以這步需要進行磁盤IO操作;現在需要查找元素:88
第一次:磁盤IO

第二次:磁盤IO
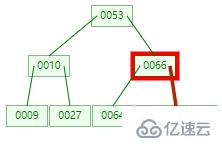
第三次:磁盤IO
然后這有一次內存比對,分別跟 70 與 88 比對,最后找到 88。
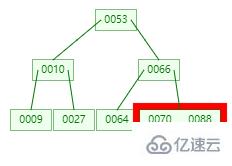
從查找過程中發現,B-tree 比對次數和磁盤IO的次數其實和二叉樹相差不了多少,這么看來并沒有什么優勢。
但是仔細一看會發現,比對是在內存中完成中,不涉及到磁盤IO,耗時可以忽略不計。
另外 B-tree 中一個節點中可以存放很多的關鍵字(個數由階決定),相同數量的關鍵字在 B-tree 中生成的節點要遠遠少于二叉樹中的節點,相差的節點數量就等同于磁盤IO的次數。這樣到達一定數量后,性能的差異就顯現出來了。
當 B-tree 要進行插入關鍵字時,都是直接找到葉子節點進行操作。
比如我們現在需要在 Max Degree(階)為 3 的 B-tree 插入元素:72
查找待插入的葉子節點
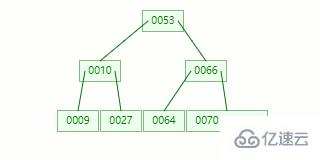
節點分裂:本來應該和 [70,88] 在同一個磁盤塊上,但是當一個節點有 3 個關鍵字的時候,它就有可能有 4 個子節點,就超過了我們所定義限制的最大度數 3,所以此時必須進行分裂:以中間關鍵字為界將節點一分為二,產生一個新節點,并把中間關鍵字上移到父節點中。
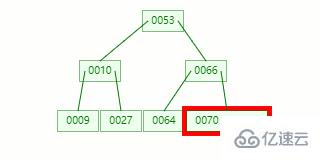
Tip : 當中間關鍵字有兩個時,通常將左關鍵字進行上移分裂。
刪除操作就會比查找和插入要麻煩一些,因為要被刪除的關鍵字可能在葉子節點上,也可能不在,而且刪除后還可能導致 B-tree 的不平衡,又要進行合并、旋轉等操作去保持整棵樹的平衡。
隨便拿棵樹(5 階)舉例子
感謝各位的閱讀!看完上述內容,你們對MySQL索引要用B+tree的原因大概了解了嗎?希望文章內容對大家有所幫助。如果想了解更多相關文章內容,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。