您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“Python協方差與相關系數怎么定義”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
聯合分布中包含了相當豐富的信息。比如從聯合分布中抽取某個隨機變量的邊緣分布,即獲得該隨機變量的分布,并可以據此,獲得該隨機變量的期望和方差。這樣做是將視線限制在單一的一個隨機變量上,我們損失了聯合分布中包含的其他有用信息,比如不同隨機變量之間的互動關系。為了了解不同隨機變量之間的關系,需要求助其它的一些描述量。
協方差(covariance)表達了兩個隨機變量的協同變化關系。我們取一個樣本空間,即學生的體檢數據。學生的身高為隨機變量X,學生的體重為隨機變量Y。
| 160cm | 170cm | 180cm | |
| 60kg | 0.2 | 0.05 | 0.05 |
| 70kg | 0.05 | 0.3 | 0.05 |
| 80kg | 0.05 | 0.05 | 0.2 |
根據上表,大的身高(180cm)和大的體重(80kg)同時出現的概率較大(0.2),小的身高值(160cm)和小的體重(60kg)的概率也較大(0.2)。偏大的身高往往伴隨偏大的體重,偏小的身高常伴隨偏小的體重。這種“大”伴隨著“大”,“小”伴隨著“小”的情形,叫做正相關。根據上面的數據,身高和體重兩個隨機變量正相關性很強。
另一方面,如果“大”配“小”,“小”配“大”的概率很高,那么兩個隨機變量負相關。“最萌身高差”是負相關的一個范例。(樣本空間為情侶的身高信息。可以定義男生身高為一個隨機變量,女生身高為另一個隨機變量)
正如其他的分布描述量一樣,協方差從概率分布中提取信息,讓我們獲知分布的“性能”。對于一個已知的聯合分布來說,任意兩個隨機變量之間都可以計算出一個協方差,即一個數值。
協方差的定義如下,如果X和Y是聯合分布的隨機變量,且分別有期望μXμX,μYμY,那么X和Y的協方差為
Cov(X,Y)=E[(X?μX)(Y?μY)]Cov(X,Y)=E[(X?μX)(Y?μY)]
協方差的定義基于期望。根據期望的定義,協方差可以直接用于離散隨機變量和連續隨機變量。
我們已經知道,期望是某個隨機變量根據概率的加權平均。我們所要加權平均的目標是X?μXX?μX和Y?μYY?μY的乘積。隨機變量和期望的差,代表了隨機變量的取值和中心值的偏離程度,也就是我們上面所謂的“偏大”或者“偏小”的情況:正值的偏離表示“偏大”,負值的偏離表示“偏小”。如果是正相關,即大配大,小配小的情況,那么這一乘積為正;如果是負相關,乘積為負。所以,通過(X?μX)(Y?μY)(X?μX)(Y?μY)這個量,我們表達了X和Y的相關性。
回到剛才的數據來計算相關性,
| 160cm | 170cm | 180cm | |
| 60kg | 0.2 | 0.05 | 0.05 |
| 70kg | 0.05 | 0.3 | 0.05 |
| 80kg | 0.05 | 0.05 | 0.2 |
讓身高為X,體重為Y。我們可以通過邊緣分布,來分別獲得X和Y的分布(回憶一下)。求得X和Y的期望,分別為170和70。計算各個格子中的(X?μX)(Y?μY)(X?μX)(Y?μY)
| 160cm | 170cm | 180cm | |
| 60kg | 100 | 0 | -100 |
| 70kg | 0 | 0 | 0 |
| 80kg | -100 | 0 | 100 |
上面的兩個表,對應的格子相乘,并求和,就得到協方差:
Cov(X,Y)=0.2×100+0.2×100+0.05×(?100)+0.05×(?100)=30(1)(2)(1)Cov(X,Y)=0.2×100+0.2×100+0.05×(?100)+0.05×(?100)(2)=30
在上面的計算中,正相關的項目都分配有比較大的概率值。最終的協方差也是一個正值。
根據期望的性質,我們可以改寫協方差的表達形式:
Cov(X,Y)=E(XY?XμX?YμX+μXμY)=E(XY)?E(X)μX?E(Y)μY+μXμY=E(XY)?E(X)E(Y)(3)(4)(5)(3)Cov(X,Y)=E(XY?XμX?YμX+μXμY)(4)=E(XY)?E(X)μX?E(Y)μY+μXμY(5)=E(XY)?E(X)E(Y)
當X和Y獨立時,有E(XY)=E(X)E(Y)E(XY)=E(X)E(Y),Cov(X,Y)=0Cov(X,Y)=0。
(注意,Cov(X,Y)=0Cov(X,Y)=0并不意味著X和Y獨立)
正的協方差表達了正相關性,負的協方差表達了負相關性。對于同樣的兩個隨機變量來說,計算出的協方差越大,相關性越強。
但隨后一個問題,身高和體重的協方差為30,這究竟是多大的一個量呢?如果我們又發現,身高與鞋號的協方差為5,是否說明,相對于鞋號,身高與體重的的相關性更強呢?
這樣橫向對比超出了協方差的能力范圍。從日常生活經驗來說,體重的上下浮動大約為20kg,而鞋號的上下浮動大約可能只是5個號碼。所以,對于體重來說,5kg與中心的偏離并不算大,而5個號碼的鞋號差距,就可能是最極端的情況了。假設身高和體重的相關強度,與身高和鞋碼的相關強度類似,但由于體重本身的數值上下浮動更大,所計算出的協方差也會更大。另一個情況,依然是計算身高與體重的協方差。數據完全不變,而只更改單位。我們的體重用克而不是千克做單位,計算出的協防差是原來數值的1000倍!
為了能進行這樣的橫向對比,我們需要排除用統一的方式來定量某個隨機變量的上下浮動。這時,我們計算相關系數(correlation coefficient)。相關系數是“歸一化”的協方差。它的定義如下:
ρ=Cov(X,Y)Var(X)Var(Y)????????????√ρ=Cov(X,Y)Var(X)Var(Y)
相關系數是用協方差除以兩個隨機變量的標準差。相關系數的大小在-1和1之間變化。再也不會出現因為計量單位變化,而數值暴漲的情況了。
依然使用上面的身高和體重數據,可以計算出
Var(X)=0.3×(60?70)2+0.3×(80?70)2=60Var(X)=0.3×(60?70)2+0.3×(80?70)2=60
Var(Y)=0.3×(180?170)2+0.3×(160?170)2=60Var(Y)=0.3×(180?170)2+0.3×(160?170)2=60
ρ=30/60=0.5ρ=30/60=0.5
這樣一個“歸一化”了的相關系數,更容易讓人把握到相關性的強弱,也更容易在不同隨機變量之間,做相關性的橫向比較。
雙變量正態分布是一種常見的聯合分布。它描述了兩個隨機變量X1X1和X2X2的概率分布。概率密度的表達式如下:
f(x1,x2)=12πσ1σ21?ρ2?????√exp[?z2(1?ρ2)]f(x1,x2)=12πσ1σ21?ρ2exp?[?z2(1?ρ2)]
其中,
z=(x1?μ1)2σ21?2ρ(x1?μ1)(x2?μ2)σ1σ2+(x2?μ2)2σ22z=(x1?μ1)2σ12?2ρ(x1?μ1)(x2?μ2)σ1σ2+(x2?μ2)2σ22
X1X1和X2X2的邊緣密度分別為兩個正態分布,即正態分布N(μ1,σ1)N(μ1,σ1), N(μ2,σ2)N(μ2,σ2)。
另一方面,除非ρ=0ρ=0,否則聯合分布也并不是兩個正態分布的簡單相乘。可以證明,ρρ正是雙變量正態分布中,兩個變量的相關系數。
我們現在繪制該分布的圖像。可惜的是,現在的scipy.stats并沒有該分布。我們需要自行編寫。
選取所要繪制的正態分布,為了簡單起見,讓μ1=0μ1=0, μ2=0μ2=0, σ1=1σ1=1,σ2=1σ2=1。
我們先讓ρ=0ρ=0,此時的聯合分布相當于兩個正態分布的乘積。繪制不同視角的同一分布,結果如下。可以看到,概率分布是中心對稱的。
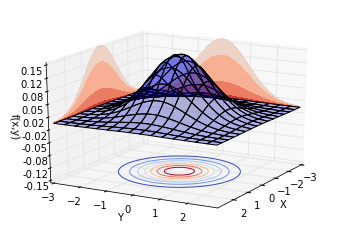
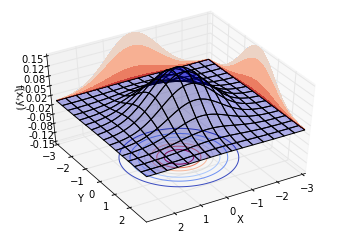
再讓ρ=0.8ρ=0.8,也就是說,兩個隨機變量的相關系數為0.8。繪制不同視角的同一分布,結果如下。可以看到,概率分布并不中心對稱。沿著Y=XY=X這條線,概率曲面隆起,概率明顯比較高。而沿著Y=?XY=?X這條線,概率較低。這也就是我們所說的正相關。
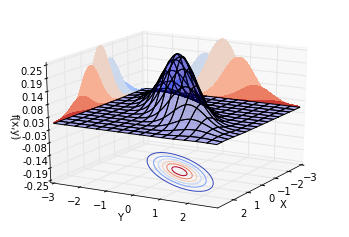
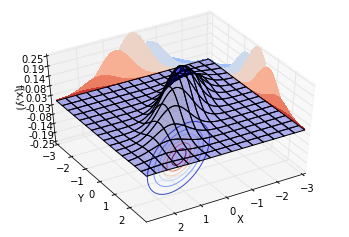
現在,ρρ對于我們來說,有了更具體的現實意義。:-)
# By Vameifrom scipy.stats import normimport numpy as np# this function is to generate a pdf of bivariate normal distributiondef bivar_norm(mu1, mu2, sigma1, sigma2, rho): # pdf of bivariate norm
def pdf(x1, x2): # get z
part1 = (x1 - mu1)**2/sigma1**2
part2 = - 2.*rho*(x1 - mu1)*(x2 - mu2)/sigma1*sigma2
part3 = (x2 - mu2)**2/sigma2**2
z = part1 + part2 + part3
cof = 1./(2.*np.pi*sigma1*sigma2*np.sqrt(1 - rho**2)) return cof*np.exp(-z/(2.*(1 - rho**2))) return pdf
pdf1 = bivar_norm(0, 0, 1, 1, 0)
pdf2 = bivar_norm(0, 0, 1, 1, 0.8)from mpl_toolkits.mplot3d import Axes3Dfrom matplotlib import cmfrom matplotlib.ticker import LinearLocator, FormatStrFormatterimport matplotlib.pyplot as plt# plot functiondef space_surface(pdf, xp, yp, zlim, rot1=30, rot2=30):
fig = plt.figure()
ax = fig.gca(projection='3d')
X = np.arange(*xp)
Y = np.arange(*yp)
X, Y = np.meshgrid(X, Y)
Z = pdf(X, Y)
surf = ax.plot_surface(X, Y, Z, rstride=8, cstride=8,
alpha = 0.3)
cset = ax.contour(X, Y, Z, zdir='z', offset=zlim[0], cmap=cm.coolwarm)
cset = ax.contourf(X, Y, Z, zdir='x', offset=xp[0], cmap=cm.coolwarm)
cset = ax.contourf(X, Y, Z, zdir='y', offset=yp[0], cmap=cm.coolwarm) for angle in range(rot1 + 0, rot1 + 360):
ax.view_init(rot2, angle)
ax.set_zlim(*zlim)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter('%.02f'))
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("f(x,y)") # fig.colorbar(surf, shrink=0.5, aspect=5)xp = [-3, 3, 0.05]
yp = [-3, 3, 0.05]
zlim1 = [-0.15, 0.15]
zlim2 = [-0.25, 0.25]
space_surface(pdf1, xp, yp, zlim1, 30, 20)
space_surface(pdf1, xp, yp, zlim1, 60, 45)
space_surface(pdf2, xp, yp, zlim2, 30, 20)
space_surface(pdf2, xp, yp, zlim2, 60, 45)“Python協方差與相關系數怎么定義”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。