溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
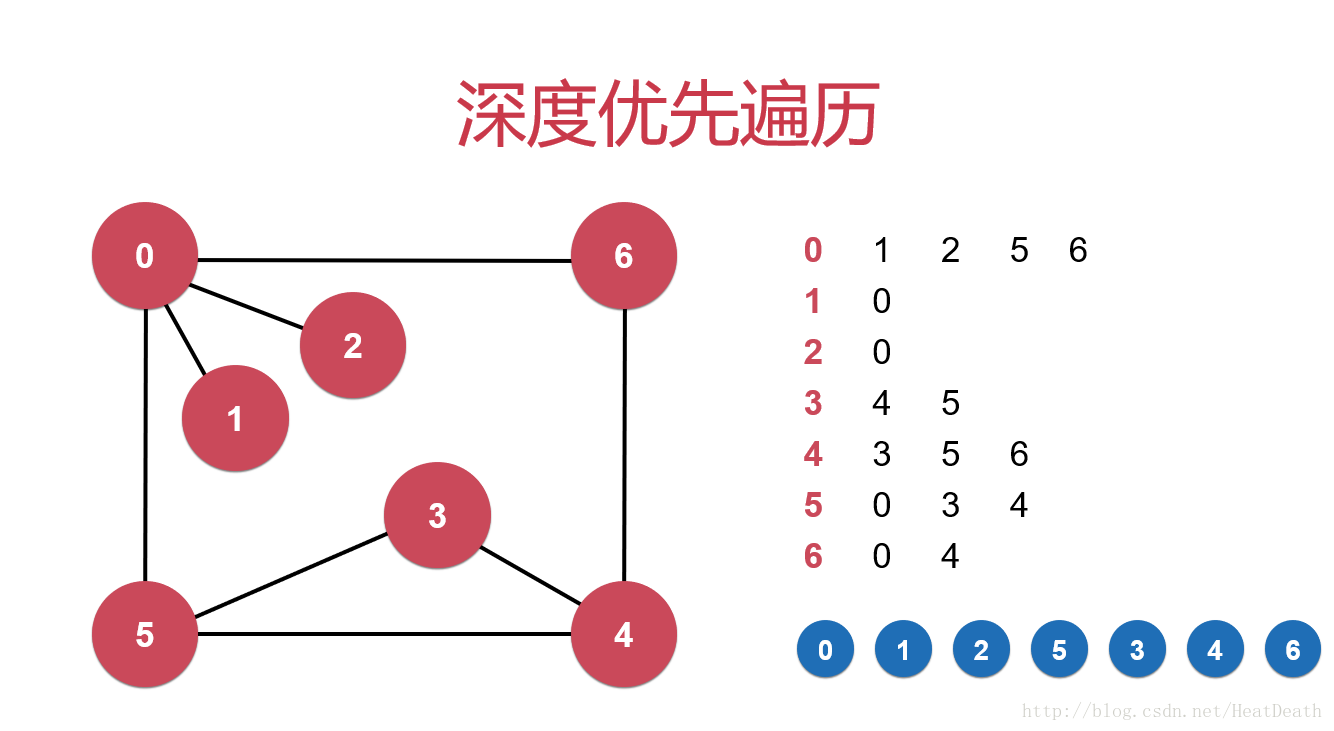
深度優先遍歷
深度優先遍歷類似于一個人走迷宮:

如圖所示,從起點開始選擇一條邊走到下一個頂點,沒到一個頂點便標記此頂點已到達。
當來到一個標記過的頂點時回退到上一個頂點,再選擇一條沒有到達過的頂點。
當回退到的路口已沒有可走的通道時繼續回退。
而連通分量,看概念:無向圖G的極大連通子圖稱為G的連通分量( Connected Component)。任何連通圖的連通分量只有一個,即是其自身,非連通的無向圖有多個連通分量。
下面看看具體實例:
package com.dataStructure.graph;
// 求無權圖的聯通分量
public class Components {
private Graph graph;
// 存放輸入的數組
private Boolean[] visited;
// 存放節點被訪問狀態
private int componentCount;
// 連通分量的數量
private int[] mark;
// 存儲節點所屬聯通分量的標記
// 構造函數,初始化私有屬性
public Components(Graph graph) {
this.graph = graph;
componentCount = 0;
// 連通分量初始數量為 0
visited = new Boolean[graph.V()];
mark = new int[graph.V()];
for (int i = 0; i < graph.V(); i++) {
visited[i] = false;
// 節點初始訪問狀態為 false
mark[i] = -1;
// 節點初始連通分量標記為 -1
}
for (int i = 0; i < graph.V(); i++) {
// 對于未被訪問的節點進行 dfs深度優先遍歷
if (!visited[i]) {
dfs(i);
componentCount++;
// 對一個節點進行dfs 到底后,一個連通分量結束,數量+1
}
}
}
private void dfs(int i) {
visited[i] = true;
// 節點 i 已被訪問
mark[i] = componentCount;
// 節點 i 屬于當前連通分量的數量(標記)
for (int node : graph.adjacentNode(i)) {
// 遍歷圖中節點 i 的鄰接節點
if (!visited[node]) // 對未被訪問的鄰接節點進行 dfs
dfs(node);
}
}
public Boolean isConnected(int v, int w) {
return mark[v] == mark[w];
// 根據兩節點所屬連通分量的標記判斷兩節點是否相連
}
public int getComponentCount() {
return componentCount;
// 返回 graph 中連通分量的數量
}
}
//public class Components {
//
// private Graph G; // 圖的引用
// private boolean[] visited; // 記錄dfs的過程中節點是否被訪問
// private int ccount; // 記錄聯通分量個數
// private int[] id; // 每個節點所對應的聯通分量標記
//
// // 圖的深度優先遍歷
// private void dfs(int v) {
//
// visited[v] = true; // 節點 v 的訪問狀態置為 true
// id[v] = ccount; // 節點 v 對應的聯通標記設置為 ccount
//
// // 遍歷節點 v 的鄰接點 i
// for (int i : G.adjacentNode(v)) {
// // 如果鄰接點 i 尚未被訪問
// if (!visited[i])
// // 對鄰接點 i 進行深度優先遍歷
// dfs(i);
// }
// }
//
// // 構造函數, 求出無權圖的聯通分量
// public Components(Graph graph) {
//
// // 算法初始化
// G = graph;
//
// // visited 數組存儲 圖G 中 節點的被訪問狀態
// visited = new boolean[G.V()];
//
// // id 數組存儲 圖G 中 節點所屬連通分量的標記
// id = new int[G.V()];
//
// // 連通分量數量初始化為 0
// ccount = 0;
//
// // 將 visited 數組全部置為 false; id 數組全部置為 -1
// for (int i = 0; i < G.V(); i++) {
// visited[i] = false;
// id[i] = -1;
// }
//
// // 求圖的聯通分量
// for (int i = 0; i < G.V(); i++)
// // 訪問一個未曾被訪問的節點
// if (!visited[i]) {
// // 對其進行深度優先遍歷
// dfs(i);
// ccount++;
// }
// }
//
// // 返回圖的聯通分量個數
// int count() {
// return ccount;
// }
//
// // 查詢點v和點w是否聯通(節點v 和 w 的聯通分量的標記是否相同
// boolean isConnected(int v, int w) {
// assert v >= 0 && v < G.V();
// assert w >= 0 && w < G.V();
// return id[v] == id[w];
// }
//}
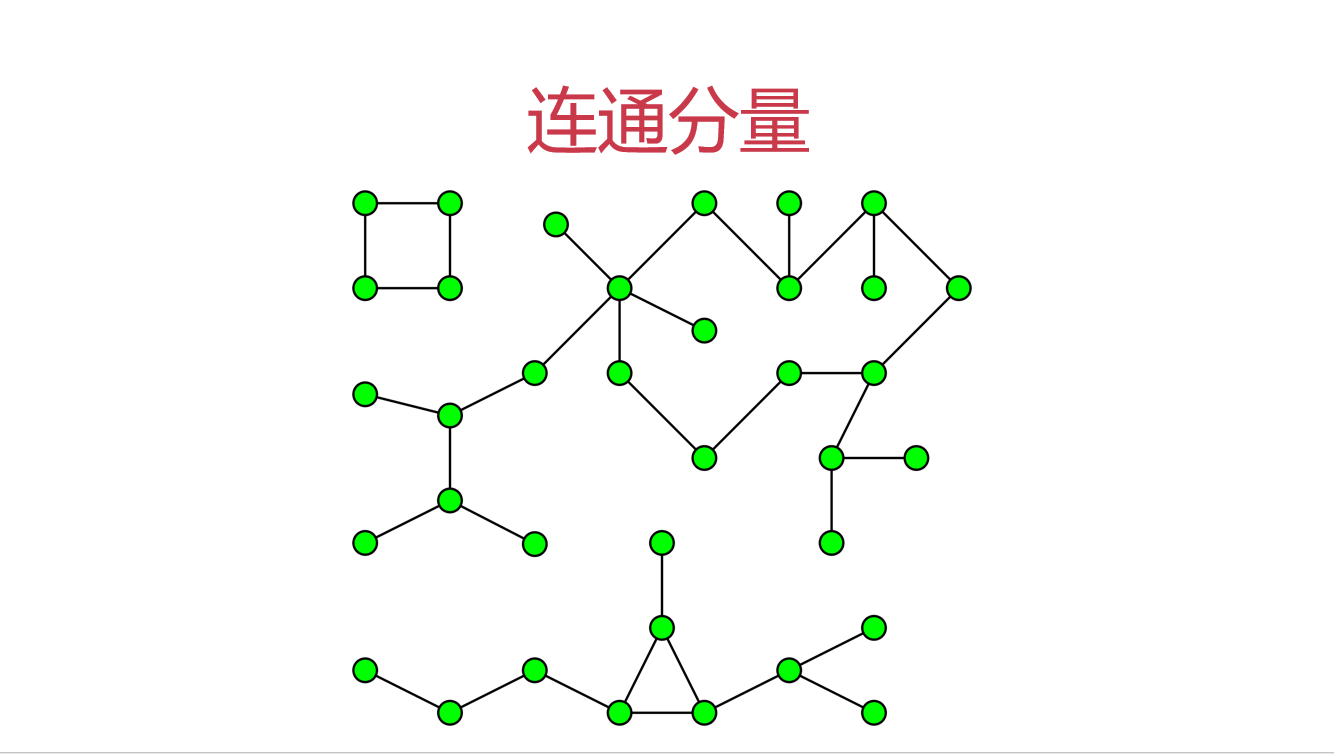
通分量數量為 3
總結
以上就是本文關于Java編程實現深度優先遍歷與連通分量代碼示例的全部內容,希望對大家有所幫助。如有不足之處,歡迎留言指出。關注億速云,您會有更多收獲。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。