您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
其實如果單從建模來講,以下大部分函數都用不到,但是這些都是基礎。
第一點:數組與矩陣概念的區分
數組:與其它編程語言一樣,定義是:相同數據類型元素的集合。
矩陣:在數學中,矩陣(Matrix)是一個按照長方陣列排列的復數或實數集合
但是需要知道的是,在matlab中經常需要使用到的是二維矩陣
接著了解一下幾個常用標點符號的原理
逗號:用來將數組中的元素分開;
分號:用來將矩陣中的行分開;
中括號:界定數組的首與尾。
行數組:如a=[1,2,3,8,-1]
列數組:b=[1;2;3;8;-1]
矩陣:A=[2,4,1;8,-2,4;2,4,6]
二 ,生成矩陣的方法有許多
目前據我所知大概有兩種,
1,先建立空矩陣a=[]
然后在工作空間點開a進入數組編輯器,進行編輯
2,用函數創建數組
(1):定步長生成法: x=a:t:b(t步長,省略的是1);
>> x=1:2:19
x =
1 3 5 7 9 11 13 15 17 19
(2):定數線性采樣法:x=linspace(a,b,n),
a,b是數組的第一個和最后一個元素,
n是采樣的總點數。
>> x=linspace(1,32,13)
x =
1 至 9 列
1.0000 3.5833 6.1667 8.7500 11.3333 13.9167 16.5000 19.0833 21.6667
10 至 13 列
24.2500 26.8333 29.4167 32.0000
3,關于數組的一些基礎函數
zeros(m):m階全零方針
zeros(m,n):m*n階全零方針
eye(m):m階單位矩陣
矩陣運算:
左除\ AX=B;X=A的-1次方乘以B
右除/ XA=B;X=B乘以A的-1次方
矩陣與常數的運算中,常數通常只能作為除數
求矩陣的逆運算(AB=BA=E(單位矩陣)),也有相應的方法;
通過函數inv可求逆運算
>> A=[1 6 9;4 2 7;8 5 3]
A =
1 6 9
4 2 7
8 5 3
>> B=eye(3)/A
B =
-0.1070 0.0996 0.0886
0.1624 -0.2546 0.1070
0.0148 0.1587 -0.0812
>> inv(A)
ans =
-0.1070 0.0996 0.0886
0.1624 -0.2546 0.1070
0.0148 0.1587 -0.0812
通過det函數可求矩陣的行列式
>> a=magic(3)
a =
8 1 6
3 5 7
4 9 2
>> det(a)
ans =
-360
矩陣的冪運算可通
指數函數expm1 expm2 expm3 expm可以很方便地完成矩陣的運算
矩陣指數是方塊矩陣的一種矩陣函數,與指數函數類似。矩陣指數給出了矩陣李代數與對應的李群之間的關系。
設X為n×n的實數或復數矩陣。X的指數,用

或exp(X)來表示,是由以下冪級數所給出的n×n矩陣:

以上的級數總是收斂的,因此X的指數是定義良好的。注意,如果X是1×1的矩陣,則X的矩陣指數就是由X的元素的指數所組成的1×1矩陣。
expm 常用矩陣指數函數
expm1 Pade法求矩陣指數
expm2 Taylor法求矩陣指數
expm3 特征值分解法求矩陣指數
這個大家有個印象就行了,記不住也沒關系,實際上一般用不到
矩陣的對數運算(logm)
矩陣的開方運算sqrtm
//以上關于對數,指數,開方運算實際運用場景并不大
magic是指行和列包括主對角線,副對角線的相加都為一個定值得函數
三,矩陣的基本函數運算
[x,y]=eig(A) 可以求出特征值和特征向量
拓展:
/*
E=eig(A):求矩陣A的全部特征值,構成向量E。
[V,D]=eig(A):求矩陣A的全部特征值,構成對角陣D,并求A的特征向量構成V的列向量。
[V,D]=eig(A,'nobalance'):與第2種格式類似,但第2種格式中先對A作相似變換后求矩陣A的特征值和特征向量,而格式3直接求矩陣A的特征值和特征向量。
E=eig(A,B):由eig(A,B)返回N×N階方陣A和B的N個廣義特征值,構成向量E。
[V,D]=eig(A,B):由eig(A,B)返回方陣A和B的N個廣義特征值,構成N×N階對角陣D,其對角線上的N個元素即為相應的廣義特征值,同時將返回相應的特征向量構成N×N階滿秩矩陣,且滿足AV=BVD。
如將特征值的取值擴展到復數領域,則一個廣義特征值有如下形式:Aν=λBν
其中A和B為矩陣。其廣義特征值(第二種意義)λ 可以通過求解方程(A-λB)ν=0,得到det(A-λB)=0(其中det即行列式)構成形如A-λB的矩陣的集合。其中特征值中存在的復數項,稱為一個“叢(pencil)”。
若B可逆,則原關系式可以寫作
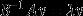
,也即標準的特征值問題。當B為非可逆矩陣(無法進行逆變換)時,廣義特征值問題應該以其原始表述來求解。
*/
奇異值函數
svd svds
范數函數
norm(X,P)
P=1,1范數
P=2, 2范數
P=inf 無窮范數
P=fro F范數
秩函數:
rank 求秩
跡函數
矩陣上所有對角線的元素之和為矩陣的跡
trace
正交空間函數
利用orth可以求矩陣的正交基
條件數函數
cond 計算矩陣的條件數的值
condest 計算矩陣的1的范數條件數的估計值
rcond 計算矩陣條件數的倒數值
偽逆函數
pinv 求解病態問題時,避免產生偽解,
通用的函數運算
funm(A,'funname')
未完待續
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。