您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
1、使用
排序
2、原理
事實上Collections.sort方法底層就是調用的array.sort方法,而且不論是Collections.sort或者是Arrays.sort方法,
跟蹤下源代碼吧,首先我們寫個demo
public static void main(String[] args) {
List<String> strings = Arrays.asList("6", "1", "3", "1","2");
Collections.sort(strings);//sort方法在這里
for (String string : strings) {
System.out.println(string);
}
}
簡單得不能再簡單的方法了,讓我們一步步跟蹤
OK,往下面看,發現collections.sort方法調用的list.sort
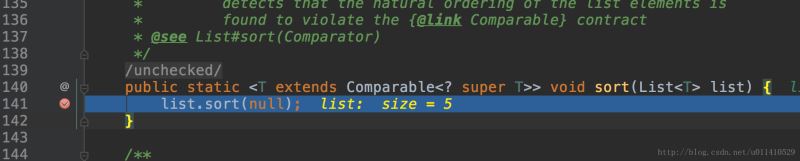
然后跟蹤一下,list里面有個sort方法,但是list是一個接口,肯定是調用子類里面的實現,這里我們demo使用的是一個Arrays.asList方法,所以事實上我們的子類就是arraylist了。OK,看arraylist里面sort實現,選擇第一個,為什么不選擇第二個呢?(可以看二樓評論,解答得很正確,簡單說就是用Arrays.sort創建的ArrayList對象)
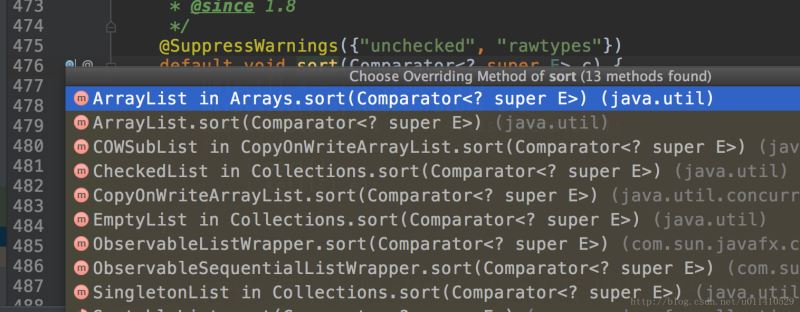
OK,發現里面調用的Arrays.sort(a, c); a是list,c是一個比較器,我們來看一下這個方法
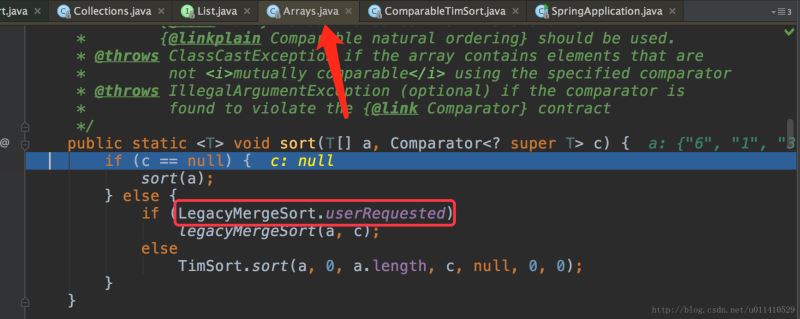
我們沒有寫比較器,所以用的第二項,LegacyMergeSort.userRequested這個bool值是什么呢?
跟蹤這個值,我們發現有這樣的一段定義:
> Old merge sort implementation can be selected (for
> compatibility with broken comparators) using a system property.
> Cannot be a static boolean in the enclosing class due to
> circular dependencies. To be removed in a future release.反正是一種老的歸并排序,不用管了現在默認是關的
OK,我們走的是sort(a)這個方法,接著進入這個
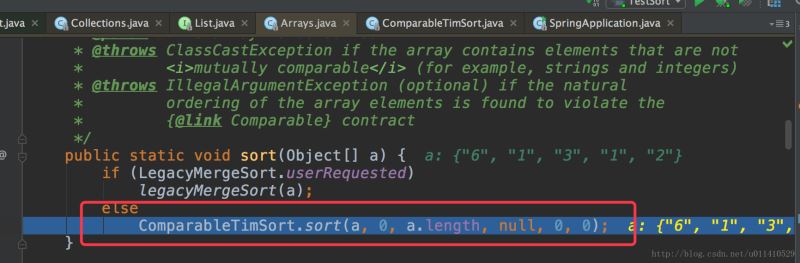
接著看我們重要的sort方法
static void sort(Object[] a, int lo, int hi, Object[] work, int workBase, int workLen) {
assert a != null && lo >= 0 && lo <= hi && hi <= a.length;
int nRemaining = hi - lo;
if (nRemaining < 2)
return; // array的大小為0或者1就不用排了
// 當數組大小小于MIN_MERGE(32)的時候,就用一個"mini-TimSort"的方法排序,jdk1.7新加
if (nRemaining < MIN_MERGE) {
//這個方法比較有意思,其實就是將我們最長的遞減序列,找出來,然后倒過來
int initRunLen = countRunAndMakeAscending(a, lo, hi);
//長度小于32的時候,是使用binarySort的
binarySort(a, lo, hi, lo + initRunLen);
return;
}
//先掃描一次array,找到已經排好的序列,然后再用剛才的mini-TimSort,然后合并,這就是TimSort的核心思想
ComparableTimSort ts = new ComparableTimSort(a, work, workBase, workLen);
int minRun = minRunLength(nRemaining);
do {
// Identify next run
int runLen = countRunAndMakeAscending(a, lo, hi);
// If run is short, extend to min(minRun, nRemaining)
if (runLen < minRun) {
int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen);
runLen = force;
}
// Push run onto pending-run stack, and maybe merge
ts.pushRun(lo, runLen);
ts.mergeCollapse();
// Advance to find next run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
// Merge all remaining runs to complete sort
assert lo == hi;
ts.mergeForceCollapse();
assert ts.stackSize == 1;
}
回到5,我們可以看到當我們寫了比較器的時候就調用了TimSort.sort方法,源碼如下
static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
T[] work, int workBase, int workLen) {
assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;
int nRemaining = hi - lo;
if (nRemaining < 2)
return; // Arrays of size 0 and 1 are always sorted
// If array is small, do a "mini-TimSort" with no merges
if (nRemaining < MIN_MERGE) {
int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
binarySort(a, lo, hi, lo + initRunLen, c);
return;
}
/**
* March over the array once, left to right, finding natural runs,
* extending short natural runs to minRun elements, and merging runs
* to maintain stack invariant.
*/
TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
int minRun = minRunLength(nRemaining);
do {
// Identify next run
int runLen = countRunAndMakeAscending(a, lo, hi, c);
// If run is short, extend to min(minRun, nRemaining)
if (runLen < minRun) {
int force = nRemaining <= minRun ? nRemaining : minRun;
binarySort(a, lo, lo + force, lo + runLen, c);
runLen = force;
}
// Push run onto pending-run stack, and maybe merge
ts.pushRun(lo, runLen);
ts.mergeCollapse();
// Advance to find next run
lo += runLen;
nRemaining -= runLen;
} while (nRemaining != 0);
// Merge all remaining runs to complete sort
assert lo == hi;
ts.mergeForceCollapse();
assert ts.stackSize == 1;
}
和上面的sort方法是一樣的,其實也就是TimSort的源代碼
3、總結
不論是Collections.sort方法或者是Arrays.sort方法,底層實現都是TimSort實現的,這是jdk1.7新增的,以前是歸并排序。TimSort算法就是找到已經排好序數據的子序列,然后對剩余部分排序,然后合并起來
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。