如何使用python實現周期方波信號頻譜圖

小編給大家分享一下如何使用python實現周期方波信號頻譜圖，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

在學習傅里葉變換的時候遇到了求周期方波信號頻譜圖的例子，在書上和網上查閱了一些資料，發現大都是討論的都是下圖左邊的周期信號的頻譜，課程老師的PPT中也只列出了另一種周期信號頻譜圖的結論，沒有在進行傅里葉變換，自己便根據定義推導了一遍，貼在這里作記錄和分享之用。

關于傅立葉級數展開的另一討論在我的另一篇文章https://www.jb51.net/article/144194.htm

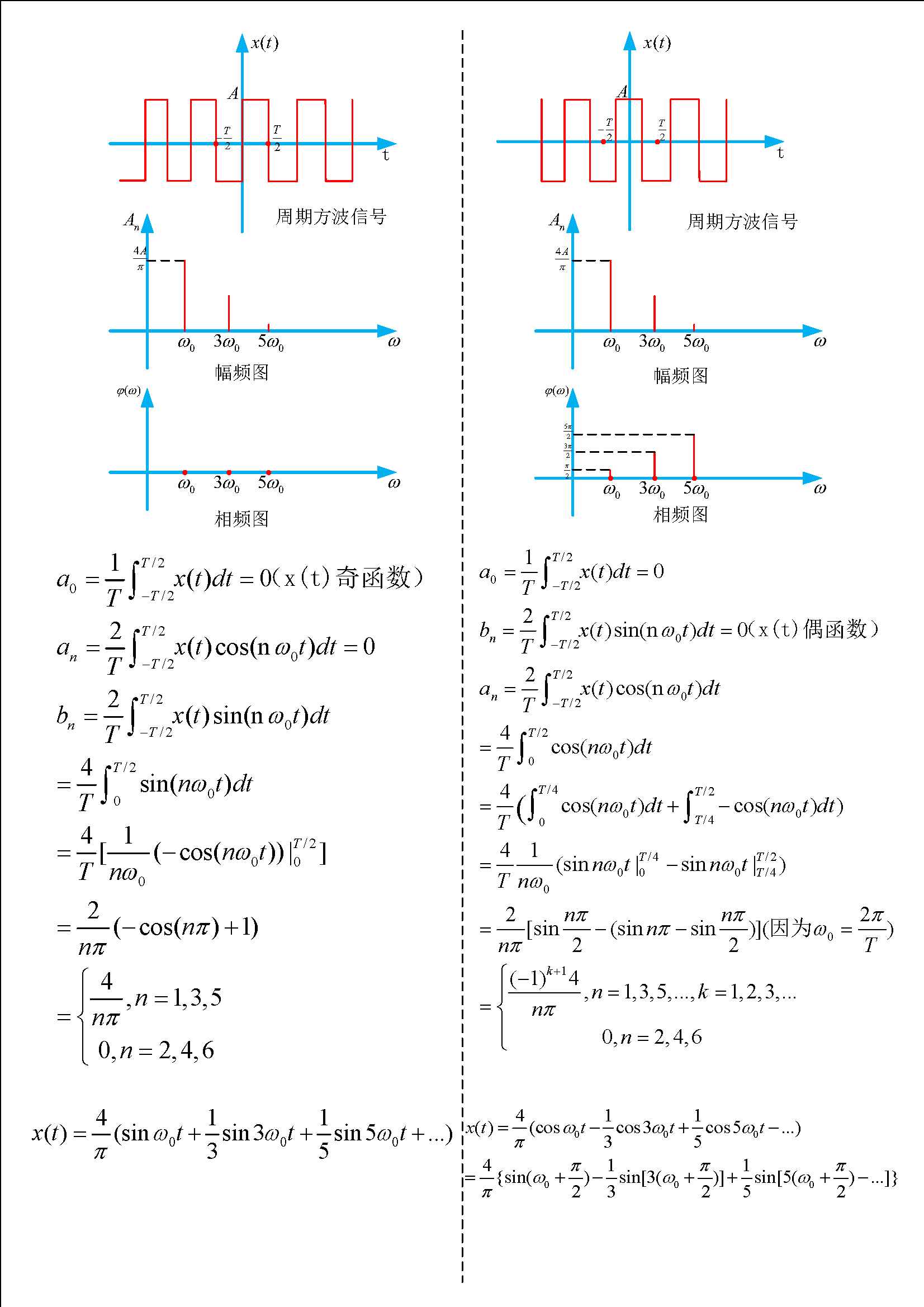
2016年11月21號更新

在第二個周期方波信號的傅里葉變換里，注意是

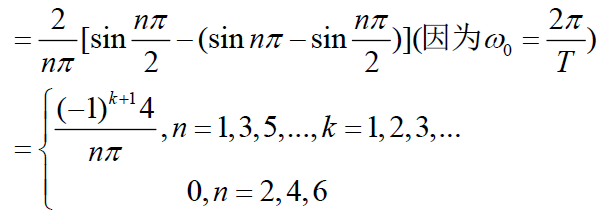
轉換為sin函數下為

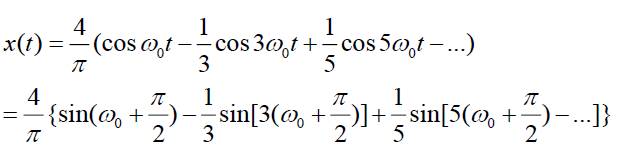
之前寫錯了，今天更正。

對于這兩種方波信號，我們也可以編程驗證一下，就是用正弦函數去逼近方波信號，Python的實現代碼如下：

# 分析傅里葉級數分解之后cos和sin的和項的圖像輸出

from numpy import mgrid,sin,cos,array,pi
from matplotlib.pyplot import plot,show,title,legend,xlabel,ylabel

x = mgrid[0:10:0.02] # 這里類似于MATLAB用冒號產生步長為0.02的序列，但是語法和MATLAB不同



# 下面的這段循環實現y=sin(x)+sin(3x)+...+sin(19x)

def cos_square():
  y1 = 0;
  for i in range(0,20,1):
    b = (-1)**(i)*cos((2*i+1)*x)/(2*i+1)
    y1=b+y1    # 這種求和的方法是從C語言移植過來的
  plot(x,y1,'orange',linewidth=0.6)
  title('cos_square')
  xlabel('Time')
  ylabel('Amplitude')
  show()

def sin_square():
  y2 = 0
  for i in range(0,20,1):
    b = sin((2*i+1)*x)/(2*i+1)
    y2=b+y2    # 這種求和的方法是從C語言移植過來的
  plot(x,y2,'g',linewidth=0.6)
  title('sin_square')
  xlabel('Time')
  ylabel('Amplitude')
  show()

cos_square() 

sin_square()

輸出結果如下：

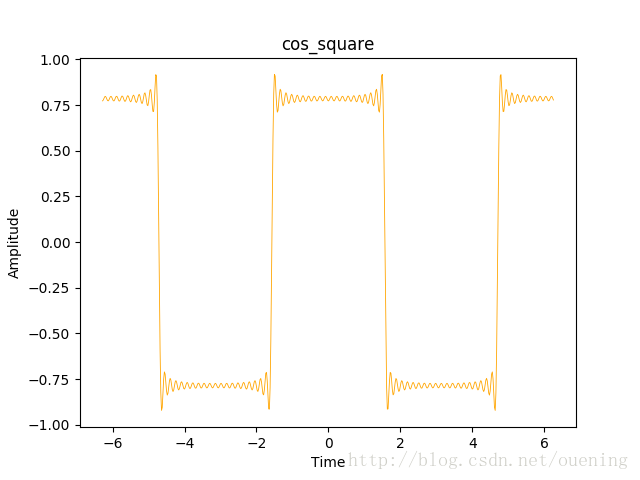
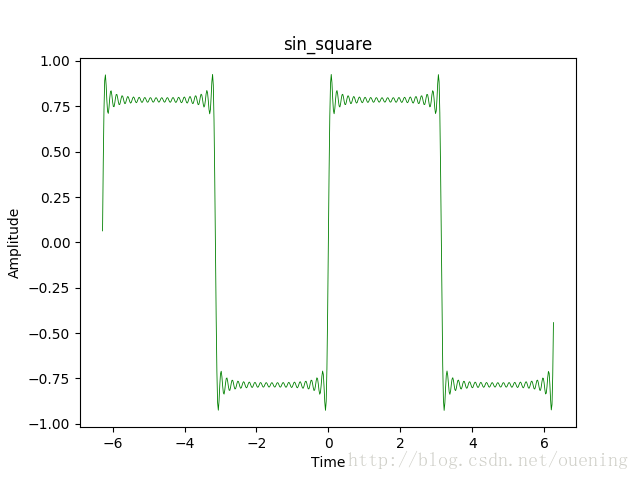
以上是“如何使用python實現周期方波信號頻譜圖”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！