您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
pytorch中的 2D 卷積層 和 2D 反卷積層 函數分別如下:
class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, groups=1, bias=True)
class torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, bias=True)
我不禁有疑問:
問題1: 兩個函數的參數為什么幾乎一致呢?
問題2: 反卷積層中的 output_padding是什么意思呢?
問題3: 反卷積層如何計算input和output的形狀關系呢?
看了中文文檔后,我得不出答案,看了英文文檔,才弄明白了。花費了一個下午的時間去研究這個問題,值得用此文紀錄一下。
我們知道,在卷積層中,輸入輸出的形狀關系為:
o = [ (i + 2p - k)/s ] +1 (1)
其中:
O : 為 output size
i: 為 input size
p: 為 padding size
k: 為kernel size
s: 為 stride size
[] 為下取整運算
(1) 當 S=1 時
若 s等于1,則公式(1)中的取整符號消失,o 與 i 為 一一對應 的關系。 我們有結論:
如果卷積層函數和反卷積層函數的 kernel_size, padding size參數相同(且 stride= 1),設反卷基層的輸入輸出形狀為 i' 和 o', 卷積層的輸入輸出形狀i和o, 則它們為 交叉對應 的關系,即:
i = o' o = i'
為回答問題3, 我們將上述關系代入公式中,即:
i' = o' + 2p - k +1
已知 i', 即可推出 o':
o' = i' - 2p + k - 1 (2)
摘兩個例子:


(2) 當 S>1 時
若 S>1 , 則公式(1)中的取整符號不能消去,o 與 i 為 多對1 的關系。 效仿 S=1時的情形, 我們有結論:
如果卷積層函數和反卷積層函數的 kernel_size, padding size參數相同(且 stride>1),設反卷基層的輸入輸出形狀為 i' 和 o', 卷積層的輸入輸出形狀i和o,
i' = [ (o' + 2p - k)/s ] +1
已知 i', 我們可以得出 s 個 o' 解:
o'(0) = ( i' - 1) x s + k - 2p o'(1) = o'(1) + 1 o'(2) = o'(1) + 2 ... o'(s-1) = o'(1) + s-1
即:
o'(n) =o'(1) + n = ( i' - 1) x s + k - 2p + n,
n = {0, 1, 2...s-1}
為了確定唯一的 o' 解, 我們用反卷積層函數中的ouput padding參數指定公式中的 n 值。這樣,我們就回答了問題(2)。
摘一個簡單的例子:
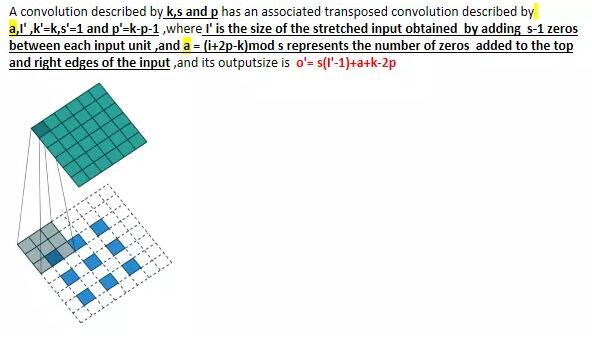
(3) 實驗驗證
給出一小段測試代碼,改變各個參數值,運行比較來驗證上面得出的結論,have fun~.
from torch import nn from torch.nn import init from torch.autograd import Variable dconv = nn.ConvTranspose2d(in_channels=1, out_channels= 1, kernel_size=2, stride=2, padding=1,output_padding=0, bias= False) init.constant(dconv.weight, 1) print(dconv.weight) input = Variable(torch.ones(1, 1, 2, 2)) print(input) print(dconv(input))
以上這篇PyTorch中反卷積的用法詳解就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。