溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
我就廢話不多說啦,直接上代碼吧!
target = [1.5, 2.1, 3.3, -4.7, -2.3, 0.75]
prediction = [0.5, 1.5, 2.1, -2.2, 0.1, -0.5]
error = []
for i in range(len(target)):
error.append(target[i] - prediction[i])
print("Errors: ", error)
print(error)
squaredError = []
absError = []
for val in error:
squaredError.append(val * val)#target-prediction之差平方
absError.append(abs(val))#誤差絕對值
print("Square Error: ", squaredError)
print("Absolute Value of Error: ", absError)
print("MSE = ", sum(squaredError) / len(squaredError))#均方誤差MSE
from math import sqrt
print("RMSE = ", sqrt(sum(squaredError) / len(squaredError)))#均方根誤差RMSE
print("MAE = ", sum(absError) / len(absError))#平均絕對誤差MAE
targetDeviation = []
targetMean = sum(target) / len(target)#target平均值
for val in target:
targetDeviation.append((val - targetMean) * (val - targetMean))
print("Target Variance = ", sum(targetDeviation) / len(targetDeviation))#方差
print("Target Standard Deviation = ", sqrt(sum(targetDeviation) / len(targetDeviation)))#標準差
補充拓展:回歸模型指標:MSE 、 RMSE、 MAE、R2
sklearn調用
# 測試集標簽預測
y_predict = lin_reg.predict(X_test)
# 衡量線性回歸的MSE 、 RMSE、 MAE、r2
from math import sqrt
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
print("mean_absolute_error:", mean_absolute_error(y_test, y_predict))
print("mean_squared_error:", mean_squared_error(y_test, y_predict))
print("rmse:", sqrt(mean_squared_error(y_test, y_predict)))
print("r2 score:", r2_score(y_test, y_predict))
原生實現
# 測試集標簽預測
y_predict = lin_reg.predict(X_test)
# 衡量線性回歸的MSE 、 RMSE、 MAE
mse = np.sum((y_test - y_predict) ** 2) / len(y_test)
rmse = sqrt(mse)
mae = np.sum(np.absolute(y_test - y_predict)) / len(y_test)
r2 = 1-mse/ np.var(y_test)
print("mse:",mse," rmse:",rmse," mae:",mae," r2:",r2)
相關公式
MSE
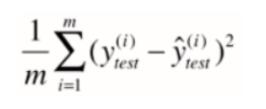
RMSE
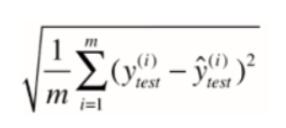
MAE
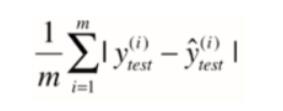
R2

以上這篇python之MSE、MAE、RMSE的使用就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。