您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了如何實現Tensorflow卷積和手寫python代碼實現卷積的方法,內容清晰明了,對此有興趣的小伙伴可以學習一下,相信大家閱讀完之后會有幫助。
從一個通道的圖片進行卷積生成新的單通道圖的過程很容易理解,對于多個通道卷積后生成多個通道的圖理解起來有點抽象。本文以通俗易懂的方式講述卷積,并輔以圖片解釋,能快速理解卷積的實現原理。最后手寫python代碼實現卷積過程,讓Tensorflow卷積在我們面前不再是黑箱子!
注意:
本文只針對batch_size=1,padding='SAME',stride=[1,1,1,1]進行實驗和解釋,其他如果不是這個參數設置,原理也是一樣。
1 Tensorflow卷積實現原理
先看一下卷積實現原理,對于in_c個通道的輸入圖,如果需要經過卷積后輸出out_c個通道圖,那么總共需要in_c * out_c個卷積核參與運算。參考下圖:
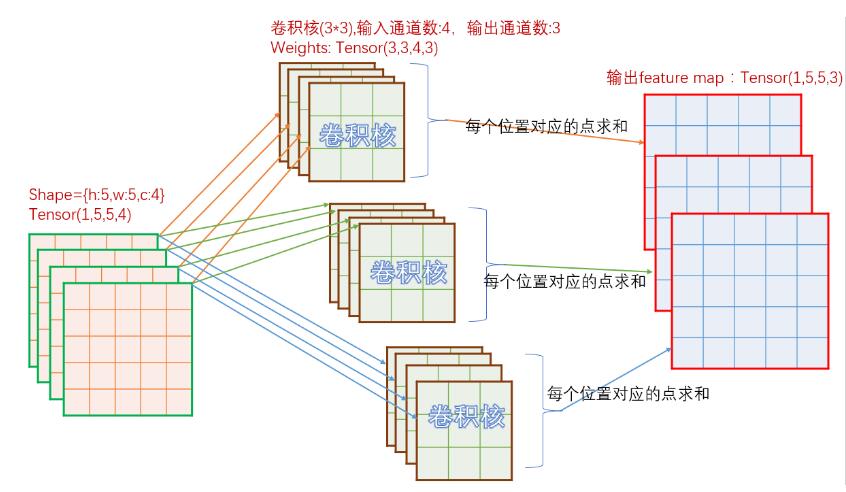
如上圖,輸入為[h:5,w:5,c:4],那么對應輸出的每個通道,需要4個卷積核。上圖中,輸出為3個通道,所以總共需要3*4=12個卷積核。對于單個輸出通道中的每個點,取值為對應的一組4個不同的卷積核經過卷積計算后的和。
接下來,我們以輸入為2個通道寬高分別為5的輸入、3*3的卷積核、1個通道寬高分別為5的輸出,作為一個例子展開。
2個通道,5*5的輸入定義如下:
#輸入,shape=[c,h,w] input_data=[ [[1,0,1,2,1], [0,2,1,0,1], [1,1,0,2,0], [2,2,1,1,0], [2,0,1,2,0]], [[2,0,2,1,1], [0,1,0,0,2], [1,0,0,2,1], [1,1,2,1,0], [1,0,1,1,1]], ]
對于輸出為1通道map,根據前面計算方法,需要2*1個卷積核。定義卷積核如下:
#卷積核,shape=[in_c,k,k]=[2,3,3] weights_data=[ [[ 1, 0, 1], [-1, 1, 0], [ 0,-1, 0]], [[-1, 0, 1], [ 0, 0, 1], [ 1, 1, 1]] ]
上面定義的數據,在接下來的計算對應關系將按下圖所描述的方式進行。
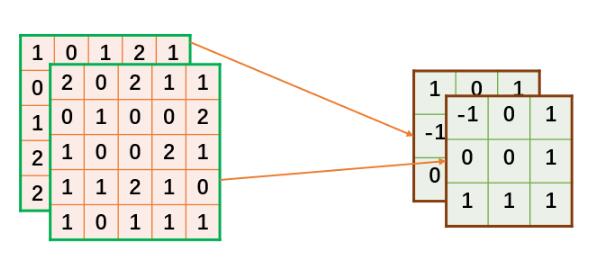
由于Tensorflow定義的tensor的shape為[n,h,w,c],這里我們可以直接把n設為1,即batch size為1。還有一個問題,就是我們剛才定義的輸入為[c,h,w],所以需要將[c,h,w]轉為[h,w,c]。轉換方式如下,注釋已經解釋很詳細,這里不再解釋。
def get_shape(tensor): [s1,s2,s3]= tensor.get_shape() s1=int(s1) s2=int(s2) s3=int(s3) return s1,s2,s3 def chw2hwc(chw_tensor): [c,h,w]=get_shape(chw_tensor) cols=[] for i in range(c): #每個通道里面的二維數組轉為[w*h,1]即1列 line = tf.reshape(chw_tensor[i],[h*w,1]) cols.append(line) #橫向連接,即將所有豎直數組橫向排列連接 input = tf.concat(cols,1)#[w*h,c] #[w*h,c]-->[h,w,c] input = tf.reshape(input,[h,w,c]) return input
同理,Tensorflow使用卷積核的時候,使用的格式是[k,k,in_c,out_c]。而我們在定義卷積核的時候,是按[in_c,k,k]的方式定義的,這里需要將[in_c,k,k]轉為[k,k,in_c],由于為了簡化工作量,我們規定輸出為1個通道,即out_c=1。所以這里我們可以直接簡單地對weights_data調用chw2hwc,再在第3維度擴充一下即可。
接下來,貼出完整的代碼:
import tensorflow as tf import numpy as np input_data=[ [[1,0,1,2,1], [0,2,1,0,1], [1,1,0,2,0], [2,2,1,1,0], [2,0,1,2,0]], [[2,0,2,1,1], [0,1,0,0,2], [1,0,0,2,1], [1,1,2,1,0], [1,0,1,1,1]], ] weights_data=[ [[ 1, 0, 1], [-1, 1, 0], [ 0,-1, 0]], [[-1, 0, 1], [ 0, 0, 1], [ 1, 1, 1]] ] def get_shape(tensor): [s1,s2,s3]= tensor.get_shape() s1=int(s1) s2=int(s2) s3=int(s3) return s1,s2,s3 def chw2hwc(chw_tensor): [c,h,w]=get_shape(chw_tensor) cols=[] for i in range(c): #每個通道里面的二維數組轉為[w*h,1]即1列 line = tf.reshape(chw_tensor[i],[h*w,1]) cols.append(line) #橫向連接,即將所有豎直數組橫向排列連接 input = tf.concat(cols,1)#[w*h,c] #[w*h,c]-->[h,w,c] input = tf.reshape(input,[h,w,c]) return input def hwc2chw(hwc_tensor): [h,w,c]=get_shape(hwc_tensor) cs=[] for i in range(c): #[h,w]-->[1,h,w] channel=tf.expand_dims(hwc_tensor[:,:,i],0) cs.append(channel) #[1,h,w]...[1,h,w]---->[c,h,w] input = tf.concat(cs,0)#[c,h,w] return input def tf_conv2d(input,weights): conv = tf.nn.conv2d(input, weights, strides=[1, 1, 1, 1], padding='SAME') return conv def main(): const_input = tf.constant(input_data , tf.float32) const_weights = tf.constant(weights_data , tf.float32 ) input = tf.Variable(const_input,name="input") #[2,5,5]------>[5,5,2] input=chw2hwc(input) #[5,5,2]------>[1,5,5,2] input=tf.expand_dims(input,0) weights = tf.Variable(const_weights,name="weights") #[2,3,3]-->[3,3,2] weights=chw2hwc(weights) #[3,3,2]-->[3,3,2,1] weights=tf.expand_dims(weights,3) #[b,h,w,c] conv=tf_conv2d(input,weights) rs=hwc2chw(conv[0]) init=tf.global_variables_initializer() sess=tf.Session() sess.run(init) conv_val = sess.run(rs) print(conv_val[0]) if __name__=='__main__': main()
上面代碼有幾個地方需要提一下,
由于輸出通道為1,因此可以對卷積核數據轉換的時候直接調用chw2hwc,如果輸入通道不為1,則不能這樣完成轉換。
輸入完成chw轉hwc后,記得在第0維擴充維數,因為卷積要求輸入為[n,h,w,c]
為了方便我們查看結果,記得將hwc的shape轉為chw
執行上面代碼,運行結果如下:
[[ 2. 0. 2. 4. 0.] [ 1. 4. 4. 3. 5.] [ 4. 3. 5. 9. -1.] [ 3. 4. 6. 2. 1.] [ 5. 3. 5. 1. -2.]]
這個計算結果是怎么計算出來的?為了讓大家更清晰的學習其中細節,我特地制作了一個GIF圖,看完這個圖后,如果你還看不懂卷積的計算過程,你可以來打我。。。。
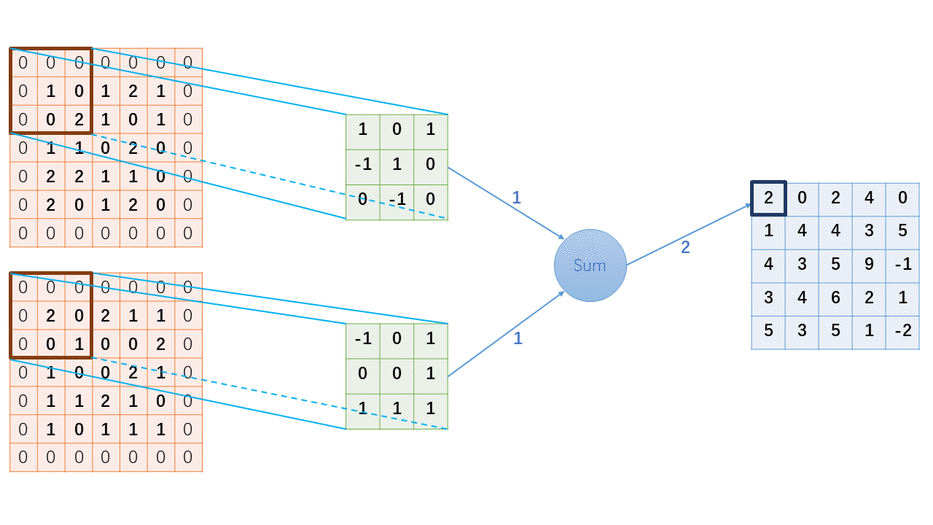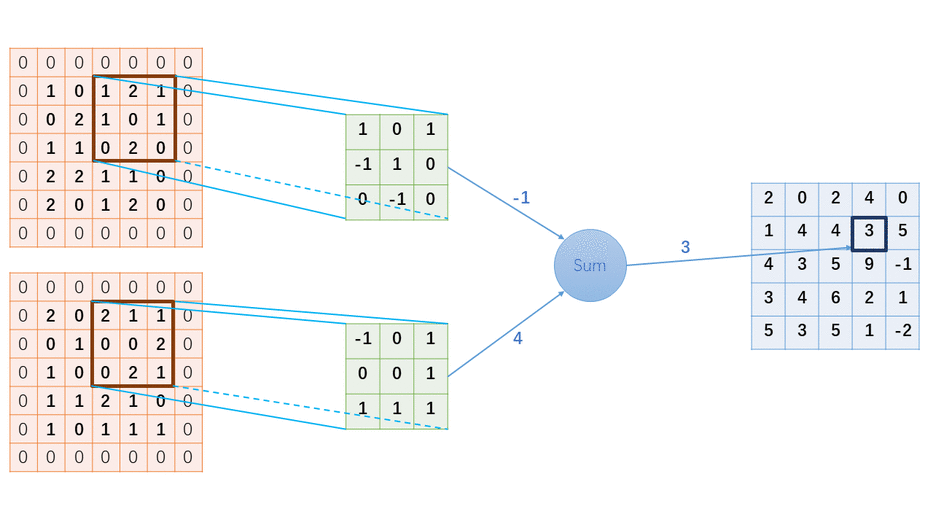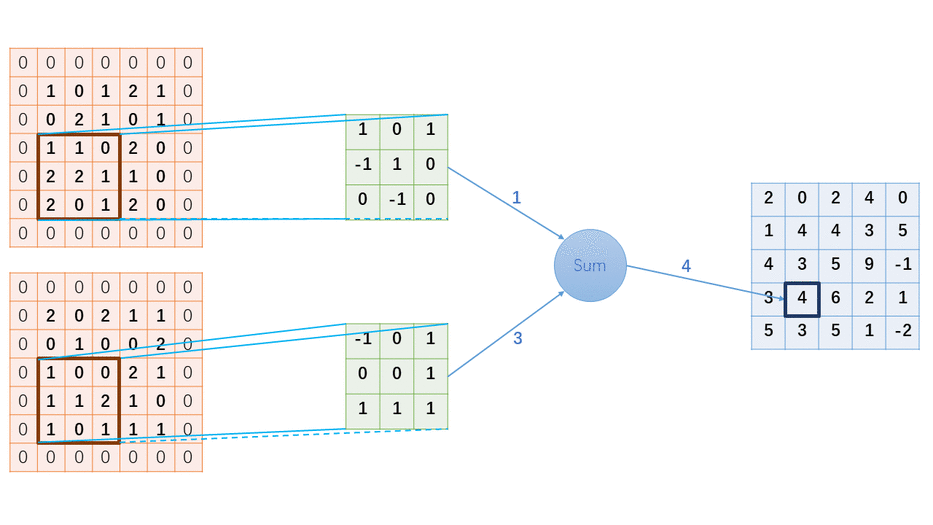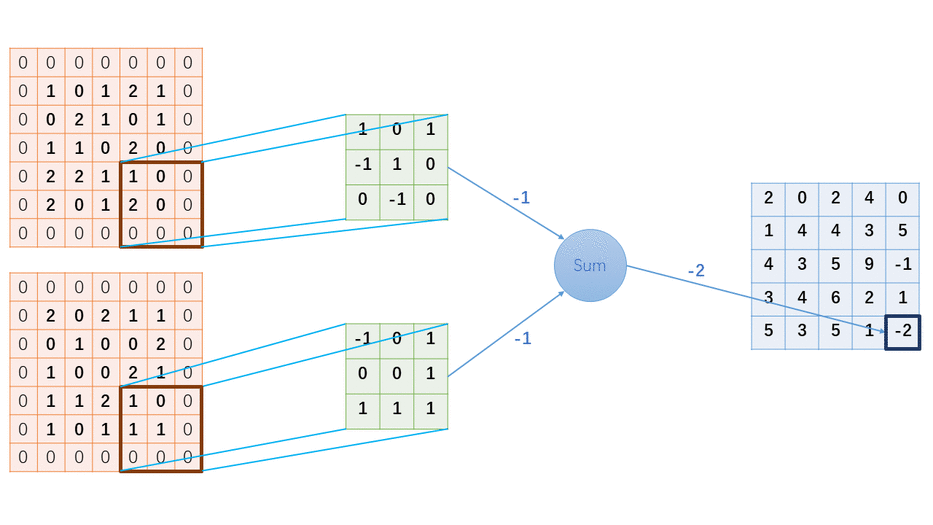
2 手寫Python代碼實現卷積
自己實現卷積時,就無須將定義的數據[c,h,w]轉為[h,w,c]了。
import numpy as np input_data=[ [[1,0,1,2,1], [0,2,1,0,1], [1,1,0,2,0], [2,2,1,1,0], [2,0,1,2,0]], [[2,0,2,1,1], [0,1,0,0,2], [1,0,0,2,1], [1,1,2,1,0], [1,0,1,1,1]] ] weights_data=[ [[ 1, 0, 1], [-1, 1, 0], [ 0,-1, 0]], [[-1, 0, 1], [ 0, 0, 1], [ 1, 1, 1]] ] #fm:[h,w] #kernel:[k,k] #return rs:[h,w] def compute_conv(fm,kernel): [h,w]=fm.shape [k,_]=kernel.shape r=int(k/2) #定義邊界填充0后的map padding_fm=np.zeros([h+2,w+2],np.float32) #保存計算結果 rs=np.zeros([h,w],np.float32) #將輸入在指定該區域賦值,即除了4個邊界后,剩下的區域 padding_fm[1:h+1,1:w+1]=fm #對每個點為中心的區域遍歷 for i in range(1,h+1): for j in range(1,w+1): #取出當前點為中心的k*k區域 roi=padding_fm[i-r:i+r+1,j-r:j+r+1] #計算當前點的卷積,對k*k個點點乘后求和 rs[i-1][j-1]=np.sum(roi*kernel) return rs def my_conv2d(input,weights): [c,h,w]=input.shape [_,k,_]=weights.shape outputs=np.zeros([h,w],np.float32) #對每個feature map遍歷,從而對每個feature map進行卷積 for i in range(c): #feature map==>[h,w] f_map=input[i] #kernel ==>[k,k] w=weights[i] rs =compute_conv(f_map,w) outputs=outputs+rs return outputs def main(): #shape=[c,h,w] input = np.asarray(input_data,np.float32) #shape=[in_c,k,k] weights = np.asarray(weights_data,np.float32) rs=my_conv2d(input,weights) print(rs) if __name__=='__main__': main()
代碼無須太多解釋,直接看注釋。然后跑出來的結果如下:
[[ 2. 0. 2. 4. 0.] [ 1. 4. 4. 3. 5.] [ 4. 3. 5. 9. -1.] [ 3. 4. 6. 2. 1.] [ 5. 3. 5. 1. -2.]]
對比發現,跟Tensorflow的卷積結果是一樣的。
看完上述內容,是不是對如何實現Tensorflow卷積和手寫python代碼實現卷積的方法有進一步的了解,如果還想學習更多內容,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。