您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
什么是算法?
算法(Algorithm)是指解題方案的準確而完整的描述,是一系列解決問題的清晰命令,算法代表著用系統的方法描述解決問題的策略機制。也就是說,能夠對一定規范的輸入,在有限時間內獲得所要求的輸出。如果一個算法有缺陷,或不適合于某個問題,執行這個算法將不會解決這個問題。不同的算法可能用不同的時間、空間或效率來完成同樣的任務。一個算法的優劣可用空間復雜度與時間復雜度來衡量。
這兩段代碼都可以稱之為算法,因為分別可以解決兩個數相加和從1加到n的問題。算法并不一定要非常復雜,小到一行代碼,多到上萬行代碼,只要能解決特定問題,就是算法。
如何評估算法優劣
使用不同算法,解決同一個問題,效率可能相差非常大
現有兩個求斐波那契數 (fibonacci number) 的算法
(斐波那契數列:1 1 2 3 5 8 ……)
這里
public static int fib1(int n) {
if (n <= 1) return n;
return fib1(n - 1) + fib1(n - 2);
}public static int fib2(int n) {
if (n <= 1) return n;
int first = 0;
int second = 1;
for (int i = 0; i < n - 1; i++) {
int sum = first + second;
first = second;
second = sum;
}
return second;
}這兩個算法哪個更優呢?
如果單從執行效率上進行評估,可能會想到這么一種方案
比較不同算法對同一組輸入的執行處理時間
這種方案也叫做:事后統計法
我們的做法是:
public static void main(String[] args) {
int n = 45;//求第45個斐波那契數
TimeTool.check("fib1", new Task() {
public void execute() {
System.out.println(fib1(n));
}
});//5.815秒
TimeTool.check("fib2", new Task() {
public void execute() {
System.out.println(fib2(n));
}
});//0.0秒
}上述方案有比較明顯的缺點
執行時間嚴重依賴硬件以及運行時各種不確定的環境因素
必須編寫相應的測算代碼
測試數據的選擇比較難保證公正性 (n=100時可能第一種算法時間更短,n=200時可能第二種算法時間更短)
一般從以下維度來評估算法的優劣
正確性、可讀性、健壯性(對不合理輸入的反應能力和處理能力)
時間復雜度(time complexity):估算程序指令的執行次數(執行時間)
空間復雜度(space complexity):估算所需占用的存儲空間
我們用這種方案評估一下計算1+2+...+n的算法

顯然第二種算法更好。難道是因為第二種方法代碼更短嗎?斐波那契數列的例子已經告訴我們并不是代碼越短越好。這個例子中第二個算法只需要三步運算就可以解決問題,而第一種需要循環n次。首先都滿足正確性、可讀性、健壯性的條件,然后從時間復雜度來講,假定一步運算的執行時間的一定的,我們考察一下大致需要執行多少次指令,就可以比較出兩種算法的時間長短;再從空間復雜度考慮,需要的變量越少、開辟的存儲空間越小,算法更好。
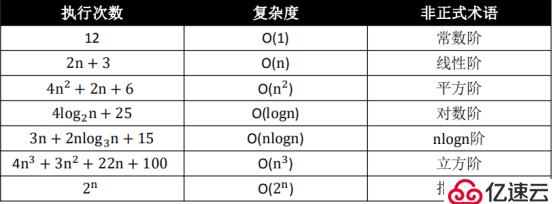
大O表示法
一般用大O表示法來描述復雜度,它表示的是數據規模 n 對應的復雜度
方法步驟:
(1)估算時間復雜度/空間復雜度(主要是時間復雜度)
(2.1)忽略常數、系數、低階
? $9$>> O(1)
? $2n+6$ >> O(n)
? $n^2+2n+6$ >> O($n^2$)
? $4n^3+3n^2+22n+100$ >> O($n^3$)
(2.2) 對數階一般省略底數
? $log_2n=log_29+log_9n$ (任意底數的對數可通過乘以一個常數相互轉化)
? 所以 $log_2n$、$log_9n$ 統稱為 $logn$
注意:大O表示法僅僅是一種粗略的分析模型,是一種估算,能幫助我們短時間內了解一個算法的執行效率
計算下面幾段代碼的時間復雜度
public static void test1(int n) {
//1(進行一次判斷操作)
if (n > 10) {
System.out.println("n > 10");
} else if (n > 5) { // 2
System.out.println("n > 5");
} else {
System.out.println("n <= 5");
}
// 1(定義一次i) + 4(i累加四次) + 4(判斷i<4四次) + 4(循環體一條語句執行四次)=9
for (int i = 0; i < 4; i++) {
System.out.println("test");
}
// 大O表示法時間復雜度O(1)
}public static void test2(int n) {
// 1(定義一次i)+ 3n(i累加n次+判斷i<n n次+循環體一條語句執行n次)=1+3n
for (int i = 0; i < n; i++) {
System.out.println("test");
}
// 大O表示法時間復雜度O(n)
}public static void test3(int n) {
// 1(定義一次i) + 2n(i累加n次+判斷i<n n次) + n(外層循環體語句執行n次) * (1(定義一次j) + 3n(j累加n次+判斷j<n n次+內層循環體一條語句執行n次))=3n^2 + 3n + 1
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
// 大O表示法時間復雜度O(n^2)
}
public static void test4(int n) {
// 8 = 2^3
// 16 = 2^4
// 3 = log2(8)
// 4 = log2(16)
// 執行次數 = log2(n)
while ((n = n / 2) > 0) {
System.out.println("test");
}
// 大O表示法時間復雜度O(logn)
}public static void test5(int n) {
// log5(n)
while ((n = n / 5) > 0) {
System.out.println("test");
}
// 大O表示法時間復雜度O(logn)
}public static void test7(int n) {
// 1(定義一次i) + 2*log2(n)(i*2運算次數) + log2(n)(外層循環執行次數) * (1 + 3n)(內層循環執行次數)
for (int i = 1; i < n; i = i * 2) {
// 1 + 3n
for (int j = 0; j < n; j++) {
System.out.println("test");
}
}
// 1 + 3*log2(n) + 2 * nlog2(n)
// 大O表示法時間復雜度O(nlogn)
}
$O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)<O(2n)<O(n!)<O(n^n)$
可以借助函數生成工具對比復雜度的大小
https://zh.numberempire.com/graphingcalculator.php
篇幅有限,在此不再過多講解。總而言之,算法的目的你可以簡單的理解為在有效的時間內用最快的方法來解答問題,這也是算法的魅力所在,吸引著無數coder為之努力。
如果您想提升自己,學習更多算法、高級編程語言技巧,這里有免費的相關學習資料,歡迎加微信:19950277730獲取更多技術提升秘籍。這里不僅有志同道合的小伙伴,更有無數免費編程技巧、學習視頻和資料,加上微信來一起探討學習技術吧!!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。