JavaScript如何實現遞歸算法

JavaScript如何實現遞歸算法？這個問題可能是我們日常學習或工作經常見到的。希望通過這個問題能讓你收獲頗深。下面是小編給大家帶來的參考內容，讓我們一起來看看吧！

我們先來看一下定義。遞歸算法，是將問題轉化為規模縮小的同類問題的子問題，每一個子問題都用一個同樣的算法去解決。一般來說，一個遞歸算法就是函數調用自身去解決它的子問題。

　　遞歸算法的特點：

1. 在函數過程中調用自身。
2. 在遞歸過程中，必須有一個明確的條件判斷遞歸的結束，既遞歸出口。
3. 遞歸算法簡潔但效率低，通常不作為推薦算法。

　　上面這些是百度百科的解釋，講的也是十分明確，大家配合實例來細細琢磨。

　　階乘

　　問題描述： n! = n*(n-1)*...2*1

　　代碼實現：

　　我們拿到問題的時候，我們按照定義的說明，可以先將規模縮小到同類的子問題。比如，n! 是等于 n* (n-1)!，然后(n-1)! = (n-1)*(n-2)!。這樣依次往下推，直到if的出口。這里用了arguments.callee，是為了防止函數名的緊密耦合，在這里它等同于factorial(n-1)。函數實現起來是不是簡潔明了呢。當然因為問題規模簡單，其實用循環也是可以實現的，大家可以嘗試一下。

斐波那契數列

　　問題描述：1, 1, 2, 3, 5, 8, 13, 21, 34, ....... 求第n個數是多少。

　　代碼實現：

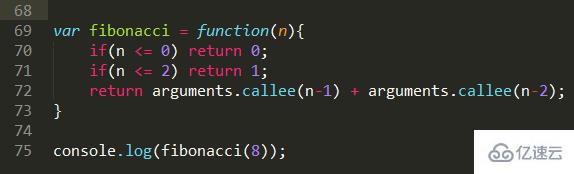
　　其實用剛才的想法實現，也是非常的簡單的。通過分析可以得到第n個數，是前兩個數的和，通過這個我們就可以通過遞歸，不斷獲得所需要的前兩個數，直到n<= 2這個條件返回1。

　　走樓梯問題

　　問題描述：樓梯有n階臺階，上樓可以一步上1階，也可以一步上2階或者3階，計算共有多少種不同的走法。

　　代碼實現：

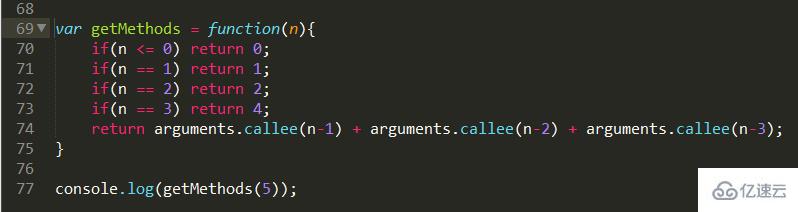
　　這其實就是一個斐波那契數列的一種實現。我們分析的時候，可以轉化成小規模的子類問題。當到達指定階梯的最后一步的時候，可以有三種種情況，一是上一步，二是上兩步，三是上三步。所以總的方法是F(n) = F(n-1) + F(n-2) + F(n-3)。然后自然就成了各自的小計算，不斷循環下去，直到判斷條件的發生。

　　最大公約數

　　問題描述：給兩個數，如果兩個數相等，最大公約數是其本身。如果不等，取兩個數相減的絕對值和兩個數中最小的數比較，相等則為最大公約，不等則繼續上面的算法，直到相等。

　　代碼實現：

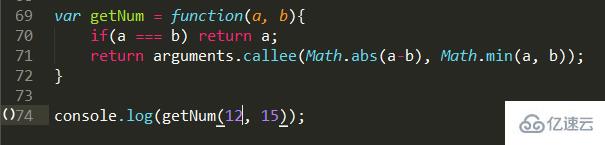
　　沒什么好說的，照問題描述所要求的實現就可以了。遞歸的出口便在于a等于b。

　漢諾塔

　　問題描述：大家都或多或少的玩過，這里就不再贅述了。

　　代碼實現：

　　在我沒有體會到遞歸的精粹前，我對這個問題簡直百思不得其解。我一直問自己，我怎么知道下一個該去哪里？后來，我就知道，我其實更關心的是，最后那一個該怎么走。這個怎么說呢？我們可以從頭想起，我們如果只有1個盤，我們可以讓它到C柱，也可以到B柱。自然兩個盤，也可以實現。3個盤，也是可以的吧。那我們就講4個盤的情況。4個盤要完成就要將A上的圓盤，完全轉移到C上。我們把前3個盤當作一個整體放到B上，然后第4個盤就可以到C上了，然后我們再將前三個放到C上，就成功了。那前三個盤，又可以重新當作一個新游戲，讓前兩個盤，當一個整體，依次類推。這樣我們只需要關心大的整體的事，其它的就轉成小規模問題解決就好了。

二分法快排

　　問題描述：使用二分法，對一個數組進行由小到大的排序。

　　代碼實現：

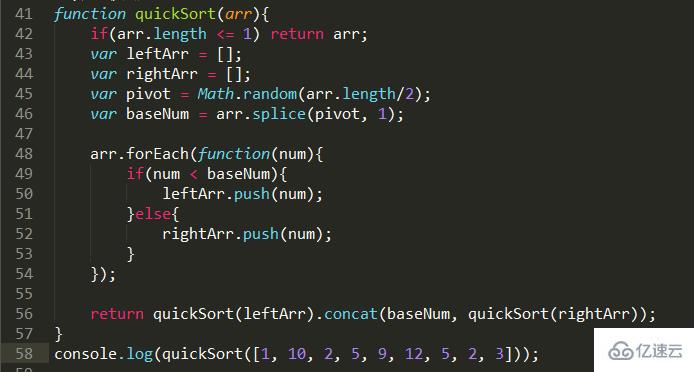
嗯...第二次寫這東西啦。這一次對遞歸的實現也是比上次清晰很多了。其實也是將大規模化為小規模，關心一個大整體，讓其不斷化為小規模進行計算。具體可以去原來那篇隨筆進行查看。

DOM樹的遞歸

問題描述：獲取一個節點的所有父節點的tagName

代碼實現：

大概都能看懂就不說什么啦。相比之前的漢諾塔和快排什么的，這個還是挺簡單的了，但是最接近我們JavaScript的實際應用。

感謝各位的閱讀！看完上述內容，你們對JavaScript如何實現遞歸算法大概了解了嗎？希望文章內容對大家有所幫助。如果想了解更多相關文章內容，歡迎關注億速云行業資訊頻道。