The Model–View Transform(模型視口變換)

周一到周五，每天一篇，北京時間早上7點準時更新~

The Model–View Transform(模型視口變換)

In a simple OpenGL application, one of the most common transformations is to take a model from model space to view space so as to render it(在OpenGL程序里，最常見的變換就是把一個模型轉到視口坐標系下去，然后渲染它). In effect, we move the model first into world space (i.e., place it relative to the world’s origin) and then from there into view space (placing it relative to the viewer)(實際上我們先把模型變換到了世界坐標系下，然后再把它變換到了視口坐標系下). This process establishes the vantage point of the scene. By default, the point of observation in a perspective projection is at the origin (0,0,0) looking down the negative z axis (into the monitor or screen)(這種處理流程就決定了觀察點的位置，在默認狀況下，觀察者的位置在投影矩陣里在0,0,0的地方，看向z軸的負方向). This point of observation is moved relative to the eye coordinate system to provide a specific vantage point(這個觀察點會相對于視口坐標系運動). When the point of observation is located at the origin, as in a perspective projection, objects drawn with positive z values are behind the observer(當觀察者位于投影坐標系的原點的時候，所有z軸正方向的東西都在觀察者后面). In an orthographic projection, however, the viewer is assumed to be infinitely far away on the positive z axis and can see everything within the viewing volume(在正交投影里，觀察者被設定為可以看到z軸的無窮遠處，所以只要在觀察者的視錐體之內，都可以被觀察者看到). Because this transform takes vertices from model space (which is also sometimes known as object space) directly into view space and effectively bypasses world space(因為這個矩陣會直接把物體從模型坐標系扔到世界坐標系里，然后直接丟進視口里去), it is often referred to as the model–view transform and the matrix that encodes this transformation is known as the model–view matrix(模型矩陣和視口矩陣的合體一般叫做模型視口矩陣). The model transform essentially places objects into world space(模型矩陣基本上就是把模型變換到世界坐標系里去). Each object is likely to have its own model transform, which will generally consist of a sequence of scale, rotation, and translation operations(每個物體基本上都包含一個模型變換，它包含了旋轉、縮放和平移). The result of multiplying the positions of vertices in model space by the model transform is a set of positions in world space. This transformation is sometimes called the model–world transform(模型矩陣乘以點能將點轉換到世界坐標系里去，所以有時候模型矩陣又叫做模型世界變換). The view transformation allows you to place the point of observation anywhere you want and look in any direction(視口變換可以讓你把觀察者放在任意位置，面向任意方向). Determining the viewing transformation is like placing and pointing a camera at the scene(定義一個視口變換就像是定義一個場景中的攝像機). In the grand scheme of things, you must apply the viewing transformation before any other modeling transformations(宏觀意義上，你必須在模型變換之前進行視口變換). The reason is that it appears to move the current working coordinate system with respect to the eye coordinate system(原因是它會相對于視口坐標系對物體進行操作). All subsequent transformations then occur based on the newly modified coordinate system(所有后續的變換都是基于當前的坐標系統進行的). The transform that moves coordinates from world space to view space is sometimes called the world–view transform(將世界坐標系的東西變換到視口坐標系的變換叫世界視口變換). Concatenating the model–world and world–view transform matrices by multiplying them together yields the model–view matrix(模型矩陣和視口矩陣結合的產物叫模型視口矩陣) (i.e., the matrix that takes coordinates from model to view space). There are some advantages to doing this(這么做是有好處的). First, there are likely to be many models in your scene and many vertices in each model(第一，你的場景中會有很多模型，模型中會有很多點). Using a singlecomposite transform to move the model into view space is more efficient than moving it first into world space and then into view space as explained earlier(使用合成矩陣比起分開會更高效). The second advantage has more to do with the numerical accuracy of single-precision floating-point numbers: The world could be huge and computation performed in world space will have different precision depending on how far the vertices are from the world origin(第二個好處就是與單精度浮點數的精度有關了：世界會很大，在世界坐標系下根據各個點離遠點的距離的不同變換的各個點的精度是不一樣的). However, if you perform the same calculations in view space, then precision is dependent on how far vertices are from the viewer, which is probably what you want— a great deal of precision is applied to objects that are close to the viewer at the expense of precision very far from the viewer(如果把他們直接轉換到視口坐標系里，精度與觀察者的距離有關，剛好符合我們的需要).

The Lookat Matrix(模型視口變換)

If you have a vantage point at a known location and a thing you want to look at, you will wish to place your your virtual camera at that location and then point it in the right direction(如果你希望在某個點看向某個方向，那么你將會希望吧虛擬攝像機放到那個點并指向那個你想看的方向). To orient the camera correctly, you also need to know which way is up; otherwise, the camera could spin around its forward axis and, even though it would still be technically be pointing in the right direction, this is almost certainly not what you want(為了知道正確的朝向，你需要知道指向頭頂的向量是什么，歡聚話來說，攝像機可能繞著它的前方轉，即便它有可能指向的是右邊的方向). So, given an origin, a point of interest, and a direction that we consider to be up, we want to construct a sequence of transforms, ideally baked together into a single matrix, that will represent a rotation that will point a camera in the correct direction and a translation that will move the origin to the center of the camera(所以，給定一個原點、一個方向、一個視點后，我們需要構造一個矩陣剛好能表達攝像機的這樣一個姿態). This matrix is known as a lookat matrix and can be constructed using only the math covered in this chapter so far.(這個矩陣叫lookat矩陣，你可以使用普通的數學知識就可以得到這個矩陣) First, we know that subtracting two positions gives us a vector which would move a point from the first position to the second and that normalizing that vector result gives us its directional(首先，我們通過向量減法，可以得到一個方向向量). So, if we take the coordinates of a point of interest, subtract from that the position of our camera, and then normalize the resulting vector, we have a new vector that represents the direction of view from the camera to the point of interest. We call this the forward vector(所以我們使用視點減去攝像機的位置，然后單位化，就得到了我們的指向前方的向量了). Next, we know that if we take the cross product of two vectors, we will receive a third vector that is orthogonal (at a right angle) to both input vectors(其次，我們知道叉乘倆向量可以得到一個與這倆向量都垂直的向量). Well, we have two vectors—the forward vector we just calculated, and the up vector, which represents the direction we consider to be upward. Taking the cross product of those two vectors results in a third vector that is orthogonal to each of them and points sideways with respect to our camera(我們讓指向前方的向量和up向量叉乘得到一個向量，這個向量依然是相對于攝像機的，我們管這個叫sideways向量). We call this the sideways vector. However, the up and forward vectors are not necessarily orthogonal to each other and we need a third orthogonal vector to construct a rotation matrix(然而，up和forward向量并不是一定要互相垂直，所以我們還需要第三個垂直的向量去構成一個旋轉矩陣). To obtain this vector, we can simply apply the same process again—taking the cross product of the forward vector and our sideways vector to produce a third that is orthogonal to both and that represents up with respect to the camera(這個第三個向量就使用向前的向量做叉積與我們剛才得到的sideway向量做叉積).These three vectors are of unit length and are all orthogonal to one another, so they form a set of orthonormal basis vectors and represent our view frame(這仨向量兩兩垂直且都是單位向量，所以他們構造成了一個正交基). Given these three vectors, we can construct a rotation matrix that will take a point in the standard Cartesian basis and move it into the basis of our camera(使用這些向量，我們可以構建一個旋轉矩陣，可以把物體轉換到視口坐標系中去). In the following math, e is the eye (or camera) position, p is the point of interest, and u is the up vector. Here we go.(接下來的數學中，e是攝像機的位置，p是視點、u是up向量，讓我們開始推導吧) First, construct our forward vector, f:(首先計算向前的向量)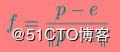

Next, take the cross product of f and u to construct a side vector s:(然后計算side向量)

Now, construct a new up vector u′ in our camera’s reference:(然后計算一個新的攝像機的向上的向量)

Finally, construct a rotation matrix representing a reorientation into our newly constructed orthonormal basis:(最后我們可以得到我們正交的旋轉矩陣了)

Finally, we have our lookat matrix, T. If this seems like a lot of steps to you, you’re in luck. There’s a function in the vmath library that will construct the matrix for you:(最后我們得到了lookat矩陣，看起來你需要做很多事，但vmath已經幫你完成了)

template
static inline Tmat4 lookat(const vecN& eye,const vecN& center,
const vecN& up) { ... }
The matrix produced by the vmath::lookat function can be used as the basis for your camera matrix—the matrix that represents the position and orientation of your camera. In other words, this can be your view matrix(vmath::lookat產生的矩陣就是你的視口矩陣了).

本日的翻譯就到這里，明天見，拜拜~~

第一時間獲取最新橋段，請關注東漢書院以及圖形之心公眾號

東漢書院，等你來玩哦