您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
????????今天我們來看下排序,那么什么是排序呢?排序是計算機內部經常進行的一種操作,其目的是將一組“無序”的數據元素調整為“有序”的數據元素。那么排序的數學定義時什么呢?如下

????????下來我們來看一個概念:排序的穩定性。什么是排序的穩定性呢?它是指如果在序列中有兩個數據元素 r[i] 和 r[j],它們的關鍵字 k[i] ?== k[j] ,且在排序之前,對象 r[i] 排在 r[j] 前面;如果在排序之后,對象 r[i] 仍在 r[j] 的前面,則稱這個排序方法是穩定的,否則稱這個排序方法是不穩定的。
????????下來我們來看看多關鍵字排序。這個就是在排序時需要比較的關鍵字多余一個,那么是什么意思呢?就是當排序結果首先按關鍵字 1 進行排序,當關鍵字 1 相同時按關鍵字 2 進行排序;...;當關鍵字 n-1 相同時按關鍵字 n 進行排序。對于多關鍵字排序,我們只需要在比較操作時同時考慮多個關鍵字即可。下來我們通過一個示例代碼來進行分析
#include?<iostream>
#include?"Object.h"
using?namespace?std;
using?namespace?DTLib;
struct?Test?:?public?Object
{
????int?key1;
????int?key2;
????Test(int?k1,?int?k2)
????{
????????key1?=?k1;
????????key2?=?k2;
????}
????bool?operator?==(const?Test&?t)
????{
????????return?(key1?==?t.key1)?&&?(key2?==?t.key2);
????}
????bool?operator?!=(const?Test&?t)
????{
????????return?!(*this?==?t);
????}
????bool?operator?>(const?Test&?t)
????{
????????return?(key1?>?t.key1)?||?((key1?==?t.key1)?&&?(key2?>?t.key2));
????}
????bool?operator?<=(const?Test&?t)
????{
????????return?!(*this?>?t);
????}
????bool?operator?<(const?Test&?t)
????{
????????return?(key1?<?t.key1)?||?((key1?==?t.key1)?&&?(key2?<?t.key2));
????}
????bool?operator?>=(const?Test&?t)
????{
????????return?!(*this?<?t);
????}
};
int?main()
{
????Test?t1(3,?4);
????Test?t2(3,?5);
????
????Test?t3(2,?4);
????Test?t4(1,?2);
????cout?<<?"t1?<?t2?:?"?<<?(t1?<?t2)?<<?endl;
????cout?<<?"t3?>?t4?:?"?<<?(t3?>?t4)?<<?endl;
????return?0;
}????????下來我們來看看輸出結果

????????在上面的示例中,我們看到排序中的關鍵操作:比較和交換。比較是指任意兩個數據元素通過比較操作確定先后次序;交換是指數據元素之間需要交換才能得到預期結果。那么我們在進行排序的時候怎么進行判斷這個排序是優是劣呢?從下面三個方面來進行判斷。1、時間性能:關鍵性能差異體現在比較和交換的數量;2、輔助存儲空間:為完成排序操作所需要額外的存儲空間,必要時可以“空間換時間”;3、算法的實現復雜性:過于復雜的排序法可能影響可讀性和可維護性。
????????下來我們來看看 DTLib 庫中的排序類的設計,如下

????????我們來基于上面的排序類來進一步實現選擇排序和插入排序。
????????1、選擇排序:它的基本思想是每次(例如第 i 次,i = 0, 1, ..., n-2)從后面 n-i 個待排的數據元素中選出關鍵字最小的元素,作為有序元素序列第 i 個元素。第 i 次選擇排序示例如下
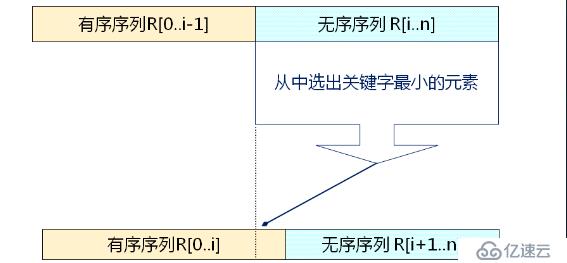
????????我們來看看具體是怎么實現的,如下所示
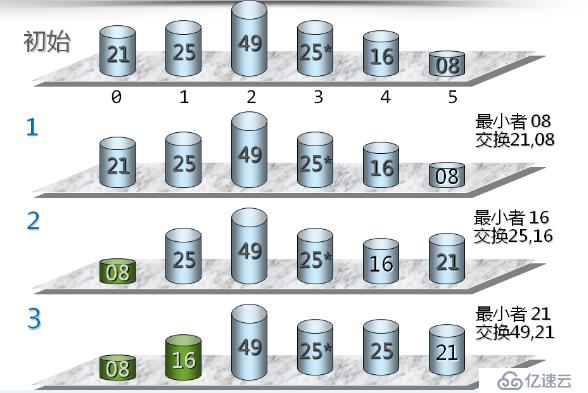
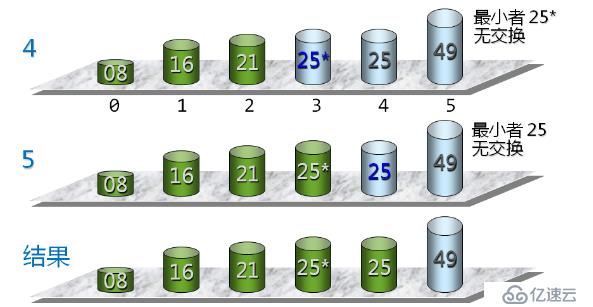
????????我們看到是從第一個開始,選出最小的數據元素,后面以此類推,直至最后全部排序完畢。下來我們來具體看看源碼是怎樣實現的
#ifndef?SORT_H
#define?SORT_H
#include?"Object.h"
namespace?DTLib
{
class?Sort?:?public?Object
{
private:
????Sort();
????Sort(const?Sort&);
????Sort&?operator=?(const?Sort&);
????template?<typename?T>
????static?void?Swap(T&?a,?T&?b)
????{
????????T?c(a);
????????a?=?b;
????????b?=?c;
????}
public:
????template?<?typename?T?>
????static?void?Select(T?array[],?int?len,?bool?min2max?=?true)
????{
????????for(int?i=0;?i<len;?i++)
????????{
????????????int?min?=?i;
????????????for(int?j=i+1;?j<len;?j++)
????????????{
????????????????if(min2max???(array[min]?>?array[j])?:?(array[min]?<?array[j]))
????????????????{
????????????????????min?=?j;
????????????????}
????????????}
????????????if(?min?!=?i?)
????????????{
????????????????Swap(array[i],?array[min]);
????????????}
????????}
????}
};
}
#endif?//?SORT_H????????測試代碼如下
#include?<iostream>
#include?"Sort.h"
using?namespace?std;
using?namespace?DTLib;
int?main()
{
????int?array[]?=?{3,?2,?4,?1,?5};
????Sort::Select(array,?5);
????for(int?i=0;?i<5;?i++)
????{
????????cout?<<?array[i]?<<?endl;
????}
}????????我們來看看運行結果
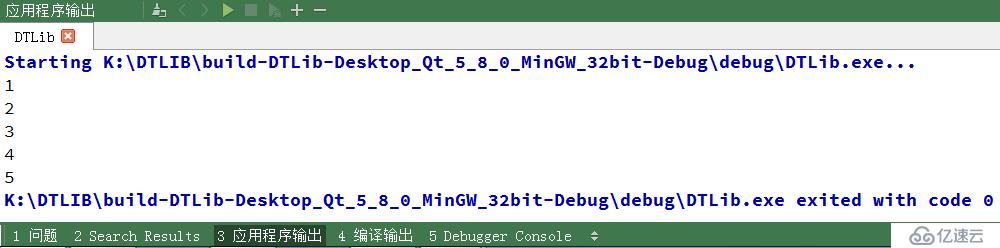
????????我們在代碼中默認是從小到大的進行排序,我們在選擇排序時,再輸入第三個參數 false,看看它是否是從大到小進行排序的
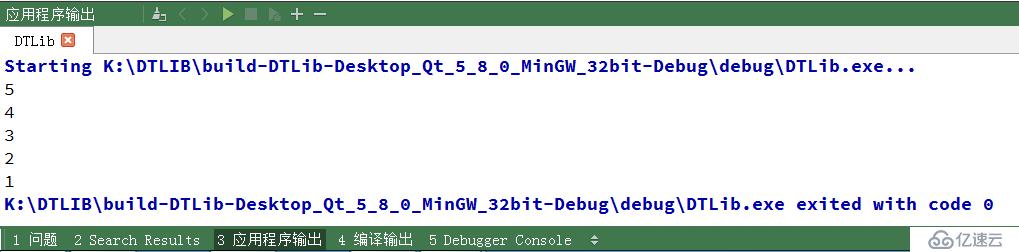
????????通過上面的排序可知,在排完序后,數據元素的位置已經改動。因此,選擇排序是不穩定排序。
????????2、插入排序:它的基本思想是當插入第 i(i >= 1) 個數據元素時,其那面的 V[0], V[1], ..., V[i-1] 已經排好序;這時,用 V[i] 的關鍵字與 V[i-1],V[i-2],...,V[0] 的關鍵字進行比較,找到位置后將 V[i] 插入,原來位置上的對象向后順移。第 i 次插入排序示例如下
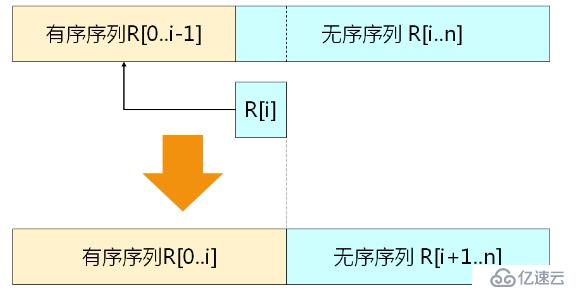
????????我們來看看具體是怎么實現的,如下所示
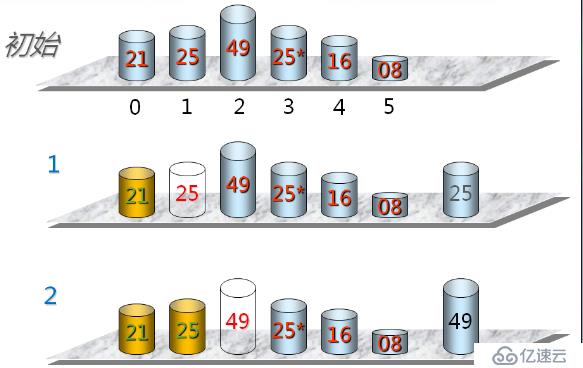

????????最后的結果為
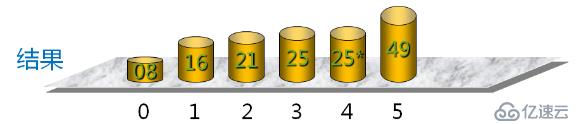
????????我們看到它是通過比較來得出具體位置的。那么我們在下面的代碼中直接從后向前來進行比較,具體源碼如下
template?<?typename?T?>
static?void?Insert(T?array[],?int?len,?bool?min2max?=?true)
{
????for(int?i=1;?i<len;?i++)
????{
????????int?k?=?i;
????????T?e?=?array[i];
????????for(int?j=i-1;?(j>=0)?&&?(min2max???(array[j]>e)?:?(array[j]<e));?j--)
????????{
????????????array[j+1]?=?array[j];
????????????k?=?j;
????????}
????????if(?k?!=?i?)
????????{
????????????array[k]?=?e;
????????}
????}
}????????我們來看看使用 Insert 排序方法是否和之前使用 Select 排序方法實現的效果是一樣的,結果如下(還是加上 false 參數)
????????我們看到效果是完全一樣的。那么根據上面的方法可知,在進行插入排序時,數據元素的相對順序不需要改動,因此插入排序是穩定排序。通過對選擇排序和插入排序的學習,總結如下:1、排序是數據元素從無序到有序的過程;2、排序具有穩定性,是選擇排序算法的因素之一;3、比較和交換是排序的基本操作,多關鍵字排序與單關鍵字排序無本質區別;4、排序的時間性能是區分排序算法好壞的主要因素;5、選擇排序每次選擇未排元素中的最小元素,插入排序每次將第 i 個元素插入前面 i-1 個已排元素中;6、選擇排序是不穩定的排序法,插入排序是穩定的排序方法;7、選擇排序和插入排序的時間復雜度為 O(n2)。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。