小球是怎么落入指定球洞的？

游戲回顧

不知大家是否還有印象，淘寶玩法平臺（一個內部系統）前不久發布了一款新的游戲 —— 小球入洞，該游戲伴隨著淘寶技術部去年雙 11 當天舉辦的一次抽獎活動，第一次在大家面前亮相。

游戲支持預先設定必中獎項：離開發射器的小球在來回彈跳一陣之后，不偏不倚的落入到指定獎項對應的球洞中。體驗該功能，可在游戲測試頁右側選項區進行如下的設置：

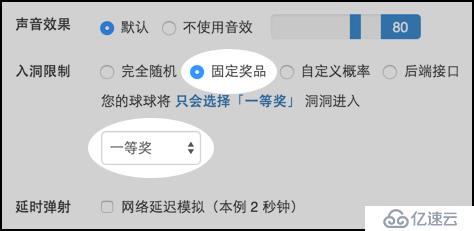
本文試著介紹游戲的這個「掉落至指定球洞」的功能，講的偏思路，并不涉及公式和代碼，我盡可能直白，如果你覺得晦澀，可以在評論處我們接著探討。在繼續之前，為了表達上的方便，我將對游戲在視覺上進行如下圖的劃分：

為什么需要指定球洞？

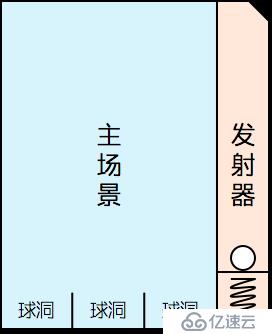
做過抽獎 UI 組件的同學都知道，抽獎結果一定是由后端計算之后返回的，原因主要有兩個：1）安全方面考慮，抽獎結果的產生過程不能在前端實現；2）只有中間服務才能更加準確的分配多端的抽獎結果。

鑒于此，所有抽獎 UI 組件都必須滿足：可事先抽得結果之后再播放動畫（顯示結果）。抽獎大轉盤便是一個很典型的例子，在轉盤滾動的時候，根據 AJAX 請求的返回，JS 其實已經知道它最終會停在哪個扇區上了。

小球入洞是一個抽獎類 UI 組件，所以當然也必須支持指定結果的抽獎，那么問題來了，小球的整個過程并不是一段簡單的動畫，怎么才能使之落入到指定球洞呢？

小球如何落入指定球洞？

如上圖示意，游戲的主場景三面環壁（小球反彈），一面布滿小洞（小球穿過），由于重力的關系，小球在有限次碰撞彈跳之后，最終一定會通過下面的小洞穿出。

「落入指定球洞」自然成了完成該游戲的第一個也是最棘手的一個難點，因為小球從發射器射出時（離開×××區域瞬間），方向是確定的（水平向左），難以從指定球洞開始，逆向地推導運動路徑并使之最終以確定的方向（水平向右）進入發射器中，此方法非常容易導致路徑太長或者無解，尋路耗時將不可控。基于逆向推導在之前也嘗試過多種優化方案，均以失敗告終。

最終采用的方式是正向推導路徑科普，即：從離開發射器開始，模擬小球的物理運動，迭代式演算，找出一條剛好能穿過指定球洞的路徑。

受場景其它物體影響（碰撞），小球的運動路徑并不能用一個公式描述出來，它的整個過程應該由多段的拋物線組成，每一次碰撞都結束一段并開始一段新的路徑，所以需要迭代法逐幀推進，才能描繪出完整路徑，下圖是一條路徑的演算過程：

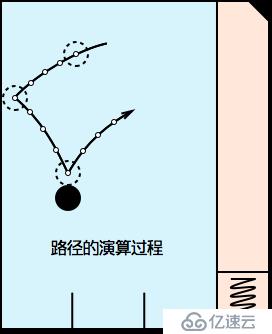
假設重力加速度、空氣阻力以及所有鋼體的彈性都是恒定的，并且墻壁和障礙物都靜止不動，小球在離開發射器之后，運動路徑就固定下來了。換句話說，影響小球軌跡的就只剩下小球離開發射器那一瞬間時的速度（離開瞬間的方向固定水平向左）。

讓小球落至指定球洞，起關鍵決定作用的就是離開發射器時的初始速度。如果能找出落向每個球洞所需的初始速度，問題就解決了。

暴破

不知怎么給這個含義扣個名堂，我估且稱之為暴破法吧，暴破即暴力破解，通常用于破解密碼，拿大量不同的鑰匙試開一把鎖，如果剛好其中一把鑰匙能打開鎖，那么暴破就成功了。

包括我在內的多數人，可能會認為暴破的時間成本很高，所以在最開始的思考中首先會自覺地把此方案屏蔽掉，在多次其它方案的實驗失敗后，我偶然一試此法，發現其實不然。

在本游戲中，我用不斷遞增的初始速度（鑰匙）來試算路徑，由于沒有 DOM 操作，且計算量并不是很大，很快就可以找出經過指定球洞（鎖）的其中一條路徑。

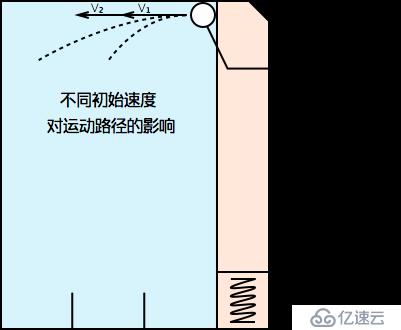
下圖是根據兩個不同初始速度試算出來的兩個不同結果：

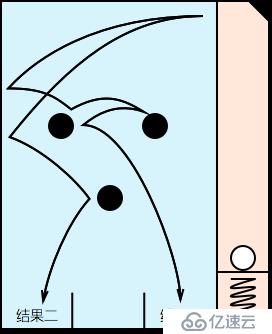
暴破的耗時有多方面的影響，本例中我用 2000 個不同的速度（從 13 到 15，步進為0.001），在某一次實驗中，跑了 10 萬次自動用例，平均一次搜索出結果嘗試次數（使用的初始速度的個數）是 11.6 次，平均一次搜索出結果用時只有 4.65ms，這個數值讓我很意外，幾乎沒有優化的必要。

在以上的 Demo 中，「搜索路徑」這個動作發生在玩家釋放彈簧之后，小球彈出之前，5ms 就消耗在這里，可以體會體會 ：）

暴破有時可以成為迅速解決問題的有效手段，比起折騰 AI 來說更加節省研發成本，對于復雜度不高的小游戲，可行性還是滿高的，也因為沒有 DOM 操作，甚至可以放在 WebWorker 里面進行。

人機對戰的臺球游戲，機器的 AI 就完全可以使用此法。

路徑拼接

搜索路徑解決了，剩下的問題就簡單得多，小球的整個運動，在本游戲中我將之分成三個階段：

• 小球彈出后，來到發射器右上拐角之前，此為第一階段，為了簡便，下文記為 A 階段；

• 小球經過拐角后，離開發射器之前，此為第二階段，也就是 B 階段；

• 小球離開發射器，直到落洞結束，此為第三階段，C 階段；

三個階段如下圖所示：

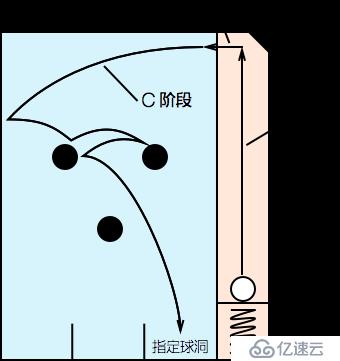
前面探討的搜索路徑一直指的都是 C 階段，為了使整個動畫看起來連貫，小球的速度變化一定得平穩，也就是：C 階段開頭的瞬時速度，等于 B 階段結尾的瞬時速度；B 階段開頭的瞬時速度，等于 A 階段結尾的瞬時速度。

如果不考慮磨擦和撞擊后的動能衰減，其實階段 A 加階段 B 在速度變化上就是自由落體的逆過程，為了簡便，我將階段 A 和階段 B 做了合并，以同一個拋物線公式（自由落體）表示，根據 C 開頭的瞬時速度，可以生成 AB 的完整路徑，這樣就得到小球的整個運動路徑了，這個過程應該好理解，不再贅述。

小插曲

由于必須落入指定球洞，所以 A 階段的初始速度自然也是固定的了，慢著！這里似乎有點兒不對勁？

彈簧的存在增加了整個過程的違合，正常人的理解，應該是彈簧壓縮得越厲害，小球射出時的初始速度越大，這跟合成路徑所需的初始速度不匹配：一個是變化的，一個是固定的。

有兩個解決辦法：

• 1）使階段 A 的初始速度受彈簧影響，利用階段 A 或階段 AB 的路程來逐漸消除該影響，使之看起來變化是平滑的；

• 2）分兩種情況：彈簧壓縮比小于 0.75 時（輕輕拉），小球初始速度受彈簧影響，但使小球彈射不成功（發出去又掉回來）；彈簧壓縮比大于 0.75 時（用力拉），小球初始速度直接等于合成路徑所需的初始速度（正常發出去）；

我采用的是后一種解決辦法，因為前一種在動畫上看起來反物理，似乎重力加速度是在變化的；而后一種方案至少彈簧壓縮比在 0-0.75 區間時都是正常的，而 0.75 以上實際體驗后違合感并不太明顯。

最后的這個問題其實正是因為非得「射入指定球洞」這件事情引起的，將這一枚小瑕疵掩藏于彈簧的這 25% 的空間里，個人感覺不算太破壞完美，所謂一快遮百丑，這就是現實版彈珠臺和電子版的區別。